Задача 63691 47,4 VTG @ 4,3 КБ/с © „! „! i . ) @&...

62337c1d4c37cb65dca2f9fa

17.03.2022 21:36:59

47,4 VTG @ 4,3 КБ/с © „! „! i . ) @& okulykkz/algebra/518/# ([ % a) 6) Рис. 471 На рисунке 47.2 изображен - график функции у f'(x). C mo- мощью графика найдите промежутки: 1) возрастания: 2) убывания; 3) знакопостоянства vA y=1'(x) vA =[x} ~ \ # : А ь// o ;/:\\\r \‚\‚ от \ > \ / AN а) 6) Рие. 472 Найдите промежутки — возрастания и убывания функции у = flx) (47.3 — 47.5) Dflx)=T7x + ; 2) fix) =3 + 8x: 3) fix)==2x - 13: 4) fix)= 10 - 4x 474. 1) &) = х * — Зх: 2) /(х) = 5х + х%; 3) fix)=8 - x% 4) fix)=x*+1 475. 1) flx) = x* = 4 2) fix) т еа 3) fix) 27 +x% 4) fix) НЧ 47.6. Докажите, что в области определения — является — возрастающ функция: A

5f3ea7e3faf909182968ddd9

19.03.2022 08:39:15

★

[b]47.2[/b]
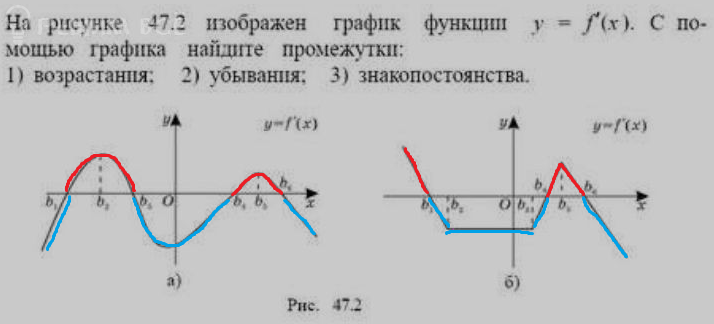
a)
f`(x) > 0 ⇒ функция y=f(x) возрастает

На рис. 47.2 а изображен график производной,

поэтому функция y=f(x) возрастает на (b_(1); b_(3)) и на (b_(4);b_(6))

f`(x) <0 ⇒ функция y=f(x) убывает

на рис. 47.2 а изображен график производной,

поэтому функция y=f(x) убывает на (- ∞ ; b_(1)) и на (b_(3);b_(4)) и на (b_(6);+ ∞ )


б)
функция возрастает ( - ∞ ; b_(1)) и на (b_(4);b_(6))

функция убывает на (b_(1); b_(4)) и на (b_(6);+ ∞ )


[b]47.3[/b]

1)

f`(x)=2х-3

f`(x) > 0 ⇒ функция y=f(x) возрастает при любом х, т.е на (- ∞ ;+ ∞ )

3)
f`(x)=-2
f`(x) < 0 ⇒ функция y=f(x) убывает при любом х, т.е на (- ∞ ;+ ∞ )


[b]47.4[/b]

1)

f`(x)=2x-3
f`(x) > 0 ⇒ 2x>3; x>3/2
функция y=f(x) возрастает на (3/2 ;+ ∞ )


f`(x) < 0 ⇒ 2x<3; x<3/2 функция y=f(x) убывает на (- ∞ ;3/2 )