Задача 63549 Построить график функции y=...
Условие
Решение
5x-1 ≠ 0
[m]x≠\frac{1}{5}[/m]
Область определения (– ∞;[m]\frac{1}{5}[/m] )U([m]\frac{1}{5}[/m] ;+ ∞ )
Это гипербола
Выделяем целую часть:
[m]y=\frac{6(x-\frac{1}{2})}{5(x-\frac{1}{5})}=\frac{6(x-\frac{1}{5}+\frac{1}{5}-\frac{1}{2})}{5(x-\frac{1}{5})}=\frac{6(x-\frac{1}{5})+6(\frac{1}{5}-\frac{1}{2})}{5(x-\frac{1}{5})}=\frac{6(x-\frac{1}{5})+6(\frac{2}{10}-\frac{5}{10})}{5(x-\frac{1}{5})}=\frac{6(x-\frac{1}{5})}{5(x-\frac{1}{5})}-\frac{(\frac{18}{10})}{5(x-\frac{1}{5})}[/m]
[m]y=\frac{6}{5}-\frac{(\frac{9}{25})}{x-\frac{1}{5}}[/m]
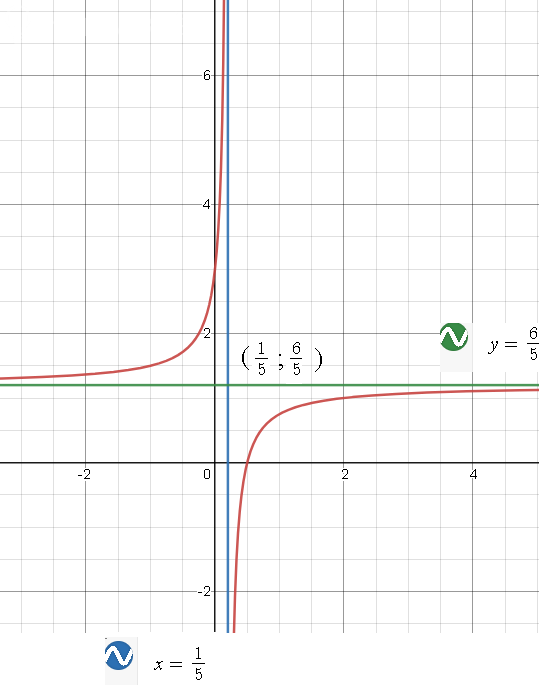
Прямая [m]x=\frac{1}{5}[/m] - вертикальная асимптота
Прямая [m]y=\frac{6}{5}[/m]- горизонтальная асимптота
Гипербола
[m]y=-\frac{(\frac{9}{25})}{x}[/m] - расположена во второй и четвертой четвертях
[m]k=-\frac{9}{25} < 0[/m]
Сдвиг вправо на [m]\frac{1}{5}[/m]
Сдвиг вверх на [m]\frac{6}{5}[/m]
[red]2 способ[/red]
Исследование функции с помощью производной
5x-1 ≠ 0
[m]x≠\frac{1}{5}[/m]
Область определения (– ∞;[m]\frac{1}{5}[/m] )U([m]\frac{1}{5}[/m] ;+ ∞ )
Прямая [m]x=\frac{1}{5}[/m] - вертикальная асимптота, так как [m] lim_{x →\frac{1}{5} }\frac{6x-3}{5x-1}= ∞ [/m]
Прямая [m]y=\frac{6}{5}[/m]- горизонтальная асимптота, так как [m] lim_{x → ∞}\frac{6x-3}{5x-1}= 3\frac{6}{5}[/m]
Функция не является ни чётной, ни нечётной,
область определения не симметрична относительно 0
и
не выполняется и вторая часть определения
[m]f(-x)=\frac{6(-x)-3}{5(-x)-1}=\frac{-6x-3}{-5x-1}=[/m]
[m]y(-x) ≠ y(x) [/m] и [m] y(-x) ≠ -y(x)[/m]
Находим производную:
[m]f`(x)=\frac{(6x-3)`\cdot (5x-1)-(6x-3)\cdot (5x-)`}{(5x-1)^2}[/m]
f` (x)> 0 на (– ∞;[m]\frac{1}{5}[/m]) и y` > 0 на ([m]\frac{1}{5}[/m];+ ∞ )
Функция возрастает на (– ∞;[m]\frac{1}{5}[/m]) и на ([m]\frac{1}{5}[/m];+ ∞ )
f`(x) ≠ 0 ⇒ Нет точек экстремума