Практика (42)
,чтобы мы могли сохранять Ваши результаты.
Решите неравенство tg(2x)>–1/√3
sinx•cosП/6
Методом понижения степени решите неравенство:
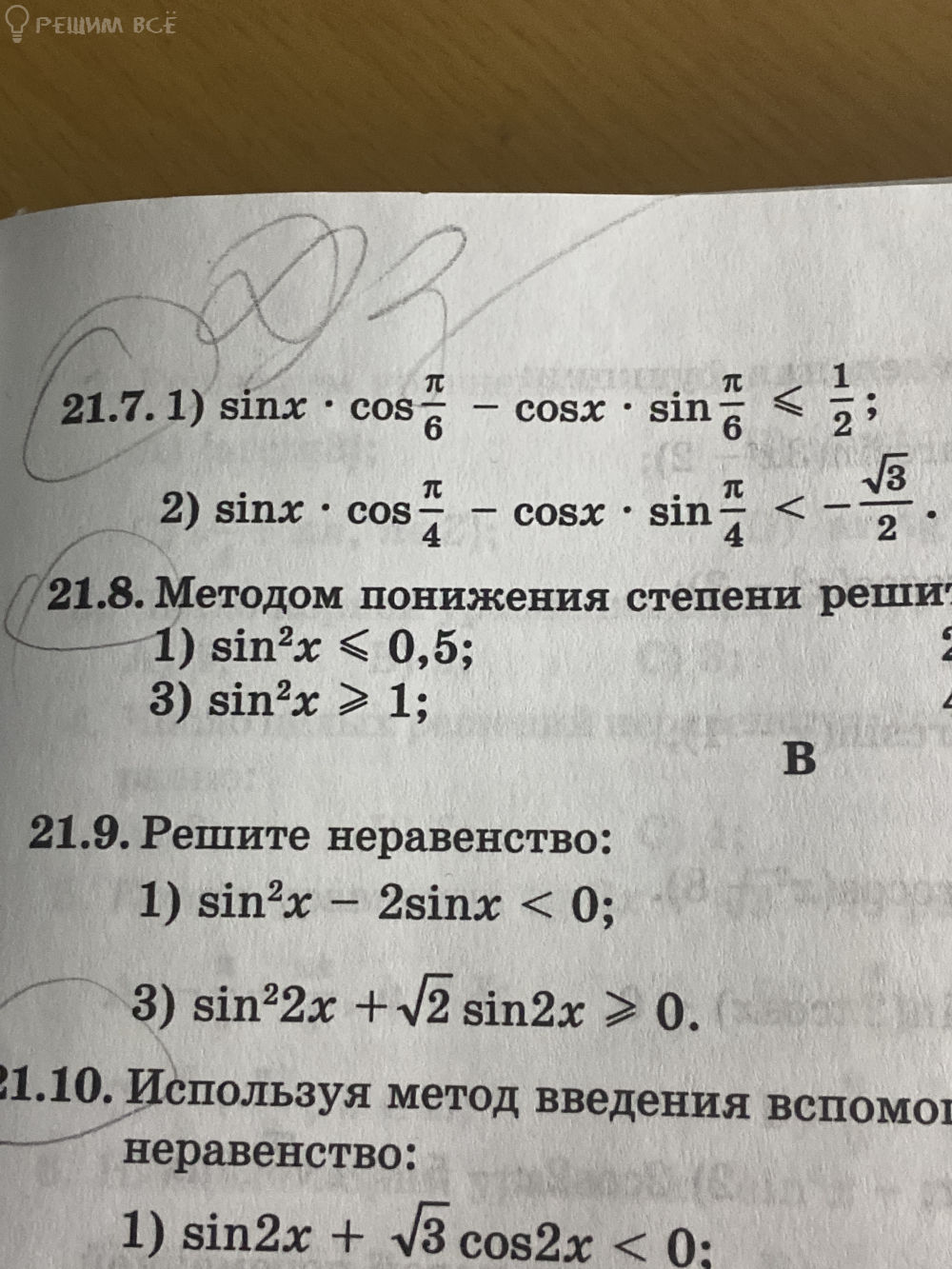
sin2x≥= 1
Sin²x>1/4; 3sinx–2cos²x<0
Решить неравенства: буду очень благодарна) можно ещё с графиком
cos2 (x/3)>3/4
–√3tg(x)<=3
2sin(x/2–п/4)≥ 1
Розв'яжи нерівність: 2sin2x−3sinx+1≤0
Відповідь: число «пі» пиши великою буквою П)
Найдите решение неравенства 2sinx < sin2x·cosx, если x принадлежит [–π/4; 3π/4]
sinx(1–2sin2x)<cos3x
(10) спасибо что помогли это последняя на сегодня задача
2cos3x ≤ 1
sin(8–2x)≥–0,5
Найдите длину отрезка, который является решением неравенства
cos² πx–sin²πх≥0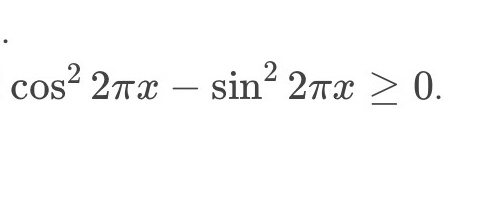
sin4 x <0.5+cos2x
Cos(3x+п/4)<1/2
3 – log₂ x
–––––––– ≥ 0
1 + cos x
1 + cos x ≠ 0
cos x ≠ –1
x ≠
a) tgx < √3
б) ctgx > 0
Sin y> –1/корень из 2
Пожалуйста срочно надо
B) tg(x–п/4)=–1 для х∈(–п/4: п/4)
С) 1+sin2x=2sinx+cosx.
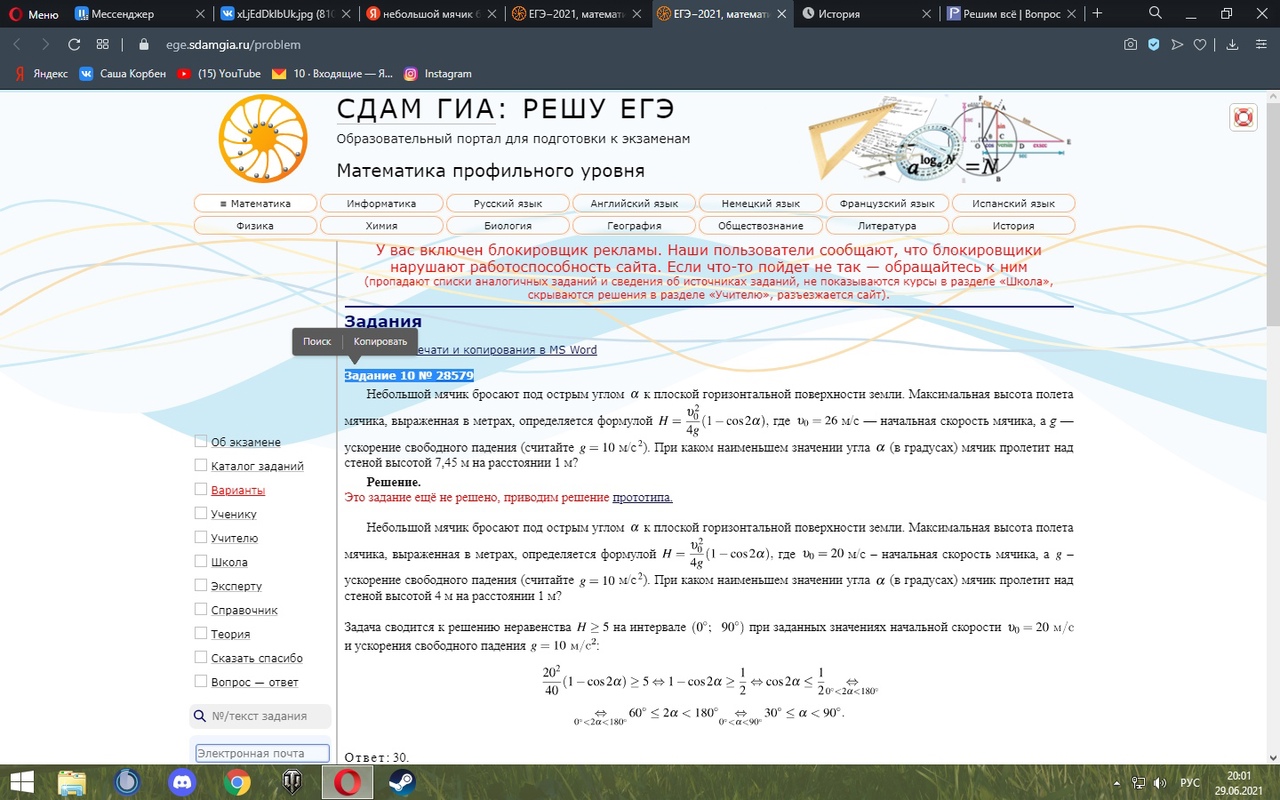
Задание 2
Решите неравенство 2sin2x–sinx–1>0.
СРОЧНОО пожалуйста
√2sin((x/2)+(π/4)) ≥ 1
используя метод введения вспомогательного аргумента, решите неравенство
1) sin2x + √3cos2x < 0
2) √3cosx – sinx > √2
3) √3cos2x+sin2x ≥ √3
sinx+sin2x+sin3x > 0
√2(sin2x–cosx) + 2sinx > 1, x ∈ [0; π]
sinx·sin2x > sin3x·sin4x
решите тригонометрические неравенства.
3)tg3x<1
4)cos(3x–п/4)<√2/2
sinxsin2x<sin3xsin4x
sinx>1/2
cosx>o
tgx>1
tgx<–1/√3
ctgx<0
tgx>–√3
ctg2x+ctgx ≥ 0
2sin2x+sinx>0
tg3x+3>3tgx+tg2x
ctg3x+2ctgx–ctg2x>2
б) sin2x+cos2xctgx>1
а) sin2x–2sinxcosx–3cos2x>0
а) sinx ≥ –√2/2
б) cos4x ≤ √3/2
1) Решите неравенства: а) 2sinx>корень из 3;
б) 2sinx ≤ 1;
2)Найдите количество целых решений неравенства
а)5sinx–2sin2 ≥ 0, принадлежащий отрезку [1;7];
б)2sinx+sin2x ≤ 0, принадлежащий отрезку [3;7];
Редакторы (1)
SOVA