Задача 59539 sin^4 x <0.5+cos2x ...
Условие
математика 10-11 класс
759
Решение
★
[b]sin^2x=(1-cos2x)/2[/b]
sin^4x=(1-cos2x)^2/4
(1-cos2x)^2/4<0,5+cos2x
1-2cos2x+cos^22x <2+4cos2x
cos^22x-6cos2x-1<0
cos2x=t
D=36-4*=32
sqrt(32)=4sqrt(2)
t_(1)=(-6-4sqrt(2))/2; t_(2)=(-6+4sqrt(2))/2
t_(1)=-3-2sqrt(2); t_(2)=-3+2sqrt(2)
⇒
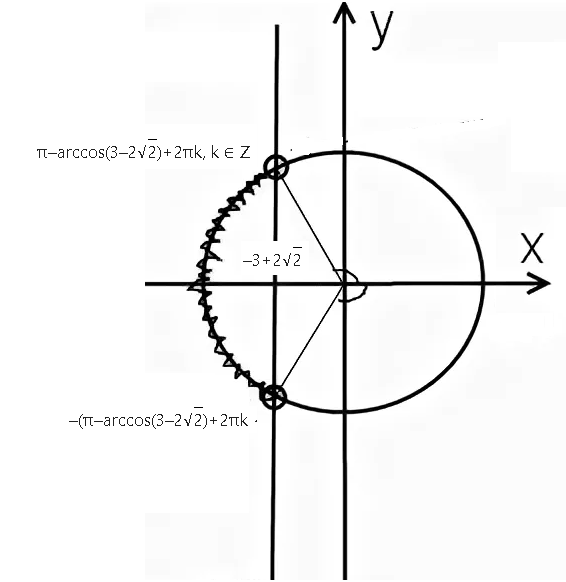
-3-2sqrt(2)<cos2x <-3+2sqrt(2)
-(π-arccos(3-2sqrt(2))+2πk < 2x < π-arccos(3-2sqrt(2))+2πk, k ∈ Z
[b]-(π/2)+(1/2)*arccos(3-2sqrt(2))+πk < x < (π/2)-(1/2) *arccos(3-2sqrt(2))+πk, k ∈ Z[/b]