Задача 55052 sinx+sin2x+sin3x > 0...
Условие
Решение
[m] (sinx+sin3x)+sin2x >0[/m]
[m] 2sin\frac{x+3x}{2}\cdot cos\frac{x-3x}{2}+sin2x >0[/m]
[m] 2sin2x \cdot cos(-x)+sin2x >0[/m]
Так как cos(-x)=cosx, то
[m] 2sin2x \cdot (2 cos+1) >0[/m]
Произведение положительно, когда множители одного знака:
[m]\left\{\begin{matrix}sin2x > 0\\cosx+\frac{1}{2} >0 \end{matrix}\right.[/m] [b] или[/b][m]\left\{\begin{matrix}
sin2x < 0\\cosx+\frac{1}{2} <0 \end{matrix}\right.[/m]
[m]\left\{\begin{matrix}sin2x > 0\\cosx>-\frac{1}{2} \end{matrix}\right.[/m] [b]или[/b][m]\left\{\begin{matrix}
sin2x < 0\\cosx<-\frac{1}{2} \end{matrix}\right.[/m]
[m]\left\{\begin{matrix} 0+2πk < 2x < π+2πk, k ∈ Z\\ -\frac{2π}{3} + 2πn < x <\frac{2π}{3} + 2πn, n ∈ Z \end{matrix}\right.[/m] [b]или[/b][m]\left\{\begin{matrix}-π+πk <2 x < 0+2πk, k ∈ Z \\\frac{2π}{3} + 2πn < x <\frac{4π}{3} + 2πn, n ∈ Z \end{matrix}\right.[/m]
[m]\left\{\begin{matrix} πk < x <\frac{π}{2}+πk, k ∈ Z\\ -\frac{2π}{3} + 2πn < x <\frac{2π}{3} + 2πn, n ∈ Z \end{matrix}\right.[/m] [b]или[/b][m]\left\{\begin{matrix}-\frac{π}{2}+πk < x < πk, k ∈ Z \\\frac{2π}{3} + 2πn < x <\frac{4π}{3} + 2πn, n ∈ Z \end{matrix}\right.[/m]
cм. рис.
[m]x ∈ (-\frac{2π}{3} + 2πm; -\frac{π}{2}+2πm) \cup (2πm; \frac{π}{2}+2πm)[/m], m ∈ Z [b]или[/b] [m] x ∈ (\frac{2π}{3} + 2πm; π+2πm)[/m], m ∈ Z
Ответ - объединение двух ответов
О т в е т. [m]x ∈ (-\frac{2π}{3} + 2πm; -\frac{π}{2}+2πm) \cup (2πm; \frac{π}{2}+2πm)\cup (\frac{2π}{3} + 2πm; π+2πm)[/m], m ∈ Z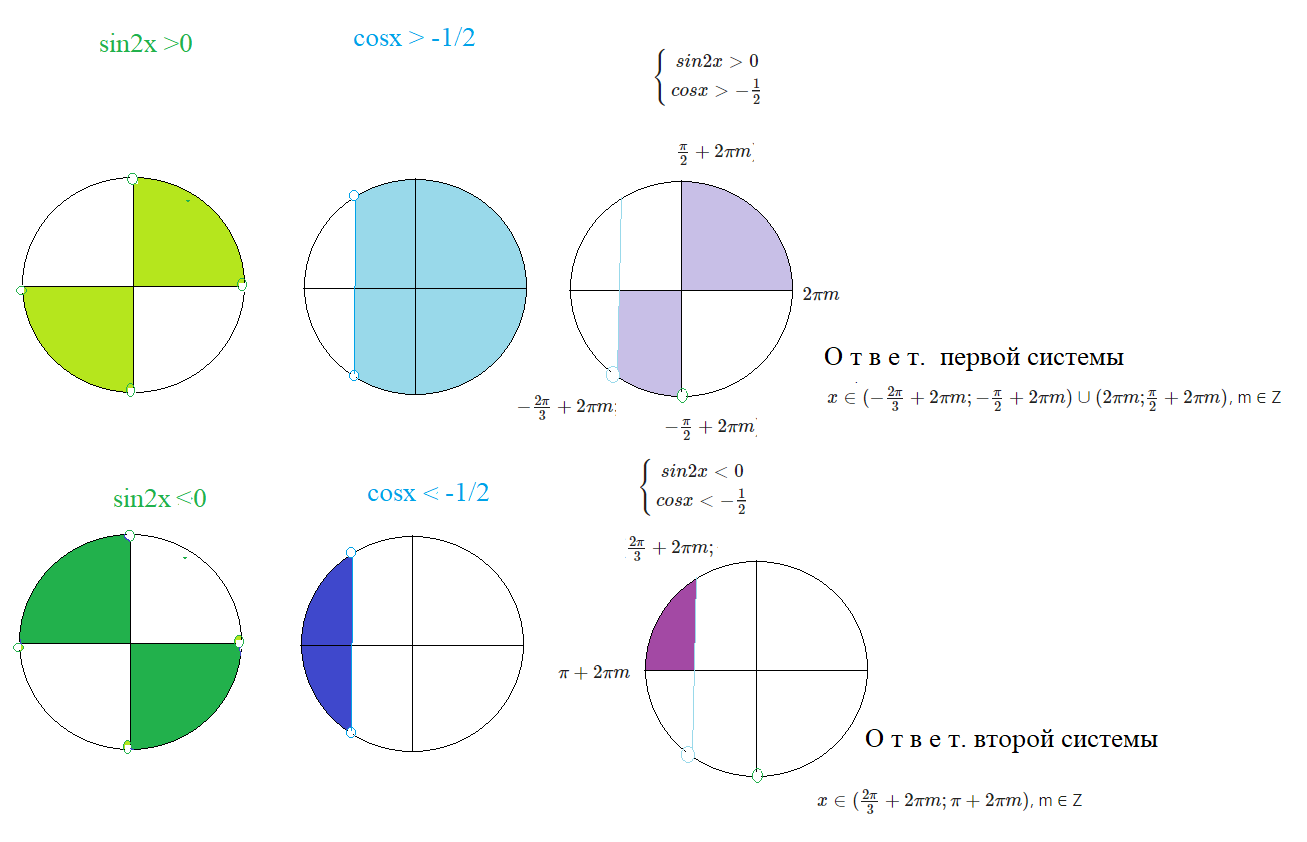
Все решения

