Задача 55306 sinx*sin2x > sin3x*sin4x...
Условие
Решение
[m] \frac{cos(x-2x)-cos(x+2x)}{2}> \frac{cos(3x-4x)-cos(3x+4x)}{2}[/m]
[m]cos(-x)-cos3x >cos(-x)-cos7x [/m]
[m]cos7x-cos3x >0[/m]
[m]-2sin\frac{7x+3x}{2}\cdot sinx\frac{7x-3x}{2} >0[/m]
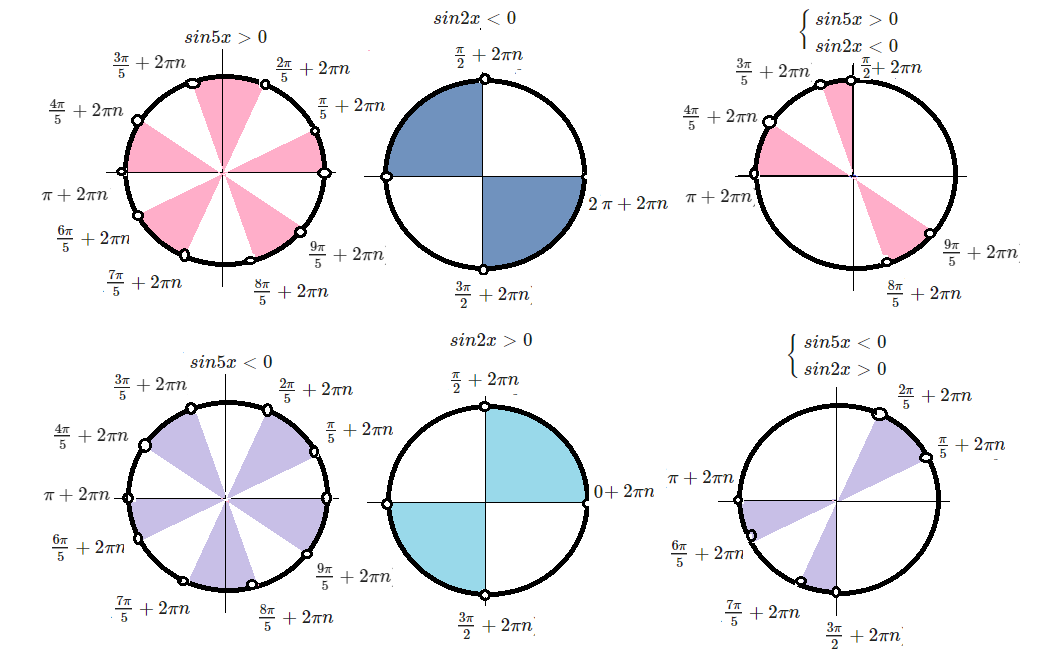
[m]sin5x \cdot sin2x <0[/m]
[m]\left\{\begin{matrix}
sin5x >0\\sin2x <0 \end{matrix}\right. [/m] или [m]\left\{\begin{matrix}
sin5x <0\\sin2x >0 \end{matrix}\right. [/m]
[m]x ∈ (\frac{π}{2}+2πn; \frac{3π}{5}+2πn)\cup (\frac{4π}{5}+2πn; π+2πn)\cup(\frac{8π}{5}+2πn;\frac{9π}{5}+2πn)[/m] или
[m]x ∈ (\frac{π}{5}+2πn; \frac{2π}{5}+2πn)\cup (π+2πn; \frac{6π}{5}+2πn)\cup(\frac{7π}{5}+2πn;\frac{3π}{2}+2πn) [/m]
О т в е т. Объединение двух ответов:
[m]x ∈ (\frac{π}{5}+2πn; \frac{2π}{5}+2πn)\cup(\frac{π}{2}+2πn; \frac{3π}{5}+2πn)\cup (\frac{4π}{5}+2πn; π+2πn)\cup[/m] [m]\cup(π+2πn; \frac{6π}{5}+2πn)\cup(\frac{7π}{5}+2πn;\frac{3π}{2}+2πn)) \cup(\frac{8π}{5}+2πn;\frac{9π}{5}+2πn)[/m]