Задача 32693 ...

vk346277623

2019-01-13 16:58:04

1) Решите неравенства: а) 2sinx>корень из 3;
б) 2sinx ≤ 1;
2)Найдите количество целых решений неравенства
а)5sinx-2sin^2 ≥ 0, принадлежащий отрезку [1;7];
б)2sinx+sin^2x ≤ 0, принадлежащий отрезку [3;7];

sova

2019-01-13 20:09:44

★

а) sinx > sqrt(3)/2
(π/3)+2πk< x < (2π/3)+2πk, k ∈ Z
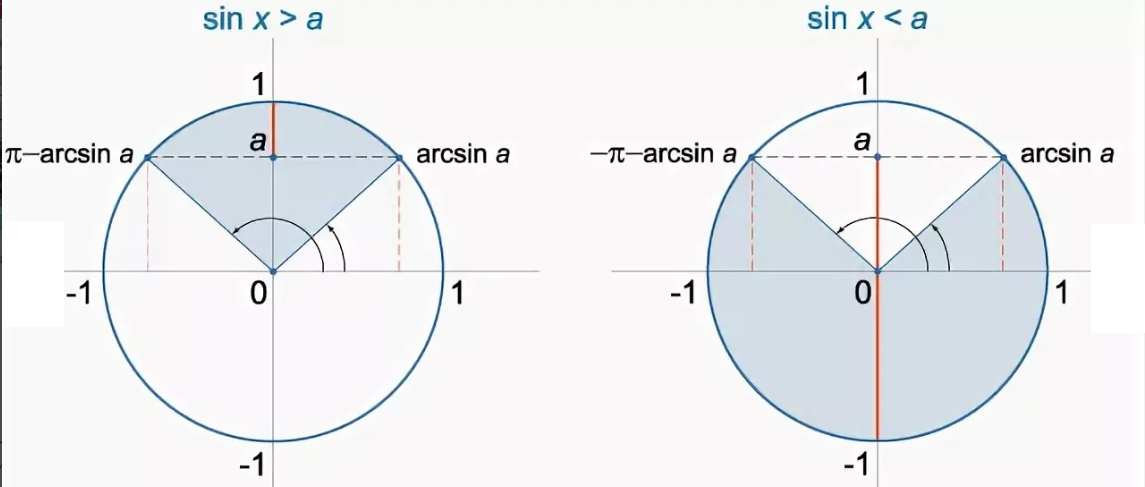
cм. рис. 1
б)
sinx ≤ 1/2
(-7π/6)+2πk ≤ x ≤ ( π/6)+2πk, k ∈ Z
см. рис.2

a)
sinx*(5-2sinx) ≥ 0

__+__ [0] _-__ [2/5] __+__

sinx ≤ 0 или sinx ≥ 2/5

[-π+2πk;0+2πk], k ∈ Z или [arcsin(2/5)+2πn, π - arcsin(2/5)+2πn], n ∈ Z

отрезку [1;7] принадлежат решения
x=1; так как arcsin(2/5) < 1 < π - arcsin(2/5)

x=2; так как arcsin(2/5) < 2 < π - arcsin(2/5)
x=3; так как arcsin(2/5) < 3 < π - arcsin(2/5)
x=7 так как 2π+arcsin(2/5) < 7 < 3π - arcsin(2/5)

б)
2sinx +sin^2x ≤ 0
sinx*(2+sinx) ≤ 0
2+sinx> 0 при любом х
sinx ≤ 0
[π+2πk; 2π+2πk], k ∈ Z

Отрезку [3;7] принадлежат корни:
х=4 так как π < 4 < 2π
х=5 так как π < 5 < 2π
х=6 так как π < 6 < 2π