Задача 65642 ...
Условие
математика 10-11 класс
389
Решение
★
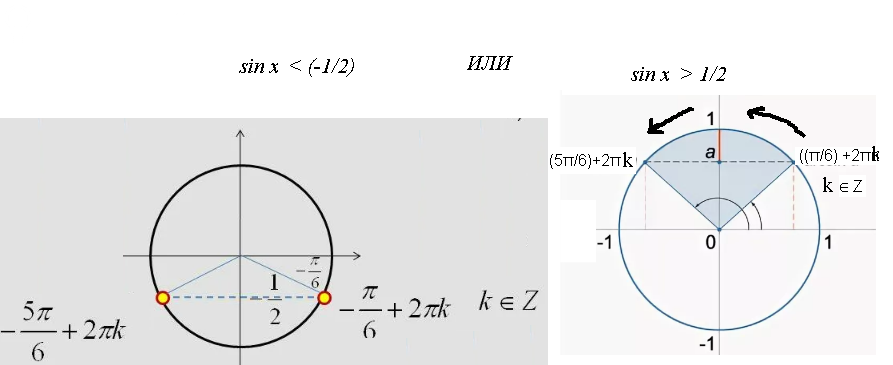
sinx < (-1/2)
((-5π/6)+2πk; (-π/6)+2πk), k ∈ [b]Z[/b]
sinx >(1/2)
((π/6)+2πn; (5π/6)+2πk),k ∈ [b]Z[/b]
Решение неравенства Sin^2x > (1/4) - объединение ответов
((-5π/6)+2πk; (-π/6)+2πk) U ((π/6)+2πn; (5π/6)+2πn), k ∈ [b]Z[/b]
см на рисунки