Задача 55347 решите тригонометрические...
Условие
3)tg3x<1
4)cos(3x-п/4)<sqrt(2)/2
Решение
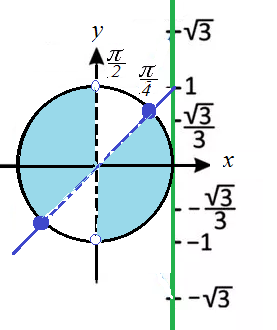
[m]-\frac{π}{2} +π k < t ≤ \frac{π}{4}+π k[/m], k ∈ Z ( см. рис. 1)
Обратный переход:
[m]-\frac{π}{2} +π k < 3x ≤ \frac{π}{4}+π k[/m], k ∈ Z
[m]-\frac{π}{6} +\frac{π}{3} k < x ≤ \frac{π}{12}+\frac{π}{3} k[/m], k ∈ Z[/b] - о т в е т
4) Замена переменной: [m]3x-\frac{π}{4}=t[/m]
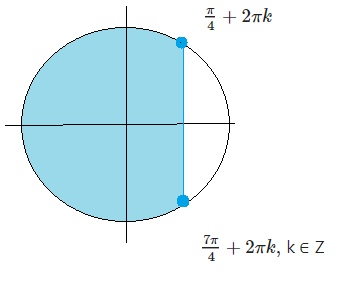
[m]\frac{π}{4} +2π k ≤ t ≤ \frac{7π}{4}+2π k,[/m]k ∈ Z ( см. рис. 2)
Обратный переход:
[m]\frac{π}{4} +2π k ≤ 3x-\frac{π}{4} ≤ \frac{7π}{4}+2π k,[/m] k ∈ Z
[m]\frac{π}{4}+\frac{π}{4} +2π k ≤ 3x ≤ \frac{7π}{4}+\frac{π}{4}+2π k,[/m] k ∈ Z
[m]\frac{π}{2}+2π k ≤ 3x ≤ 2π+2π k,[/m] k ∈ Z
[m]\frac{π}{6}+\frac{2π}{3} k ≤ x ≤\frac{2π}{3}+\frac{2π}{3} k,[/m] k ∈ Z - о т в е т