Задача 56533 ...
Условие
B) tg(x–п/4)=–1 для х∈(–п/4: п/4)
С) 1+sin2x=2sinx+cosx.
Задание 2
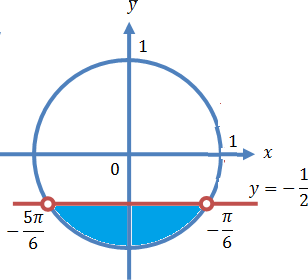
Решите неравенство 2sin2x–sinx–1>0.
СРОЧНОО пожалуйста
10-11 класс
820
Решение
★
x-(π/4))=-(π/4)+πk, k ∈ Z
x=πk, k ∈ Z
При k=0 получаем x=0 ∈ (–п/4: п/4)
2.
[blue]ЗАМЕНА ПЕРЕМЕННОЙ[/blue]
sin^2x=t
[red][b]-1 ≤ t ≤ 1[/b][/red]
2t^2-t-1 >0
D=1+8=9
t_(1)=-1/2; t_(2)=1
t < -1/2 Или t > 1 ( не удовл [red][b]-1 ≤ t ≤ 1[/b][/red])
sinx < -1/2 ⇒
-(5π/6)+2πk < x < (-π/6)+2πk, k ∈ Z