Задача 45938 а) sin^2x-2sinxcosx-3cos^2x>0 ...

marinichvika15

2020-04-03 20:40:50

а) sin^2x-2sinxcosx-3cos^2x>0

sova

2020-04-03 21:11:10

★

Пусть cosx=0, тогда sin^2x-2*sinx*0-3*0 >0 - верно [b]x=(π/2)+πk, k ∈ Z[/b] являются решениями неравенства

Пусть cosx ≠ 0, тогда
cos^2x(tg^2x-2tgx-3)>0

cos^2x>0

и
tg^2x-2tgx-3>0

D=4+12=16

корни -1 и 3

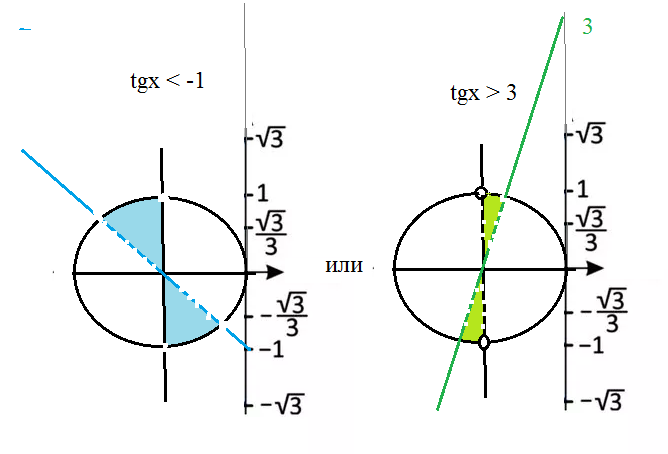
tgx < -1 или tg x > 3

[b](-π/2)+πn < x < (-π/4)+πn [/b] или [b] arctg (1/3) +πn < x < (π/2)+πn, n ∈ Z[/b]

Объединяя ответы получаем

О т в е т. [(-π/2)+πn ; (-π/4)+πn)U(arctg (1/3) +πn; (π/2)+πn], n ∈ Z