Задача 45941 ctg^3x+2ctgx-ctg^2x>2 ...

marinichvika15

3 апреля 2020 г. в 20:51

ctg³x+2ctgx–ctg²x>2

sova

3 апреля 2020 г. в 21:24

★

ctg³x+2ctgx–ctg²x–2>0
(ctg³x–ctg²x)+(2ctgx–2) >0
ctg²x·(ctgx–1)+2(ctgx–1) >0
(ctgx–1)·(ctg²x+2) >0

сtg²x+1 > 0 при любом х, сtg²x ≥ 0, 0+1 >0

ctgx–1 >0

ctgx>1
πn <x<(π/4)+πn, n ∈ Z – это ответ.

Можно так записать (πn ;(π/4)+πn), n ∈ Z

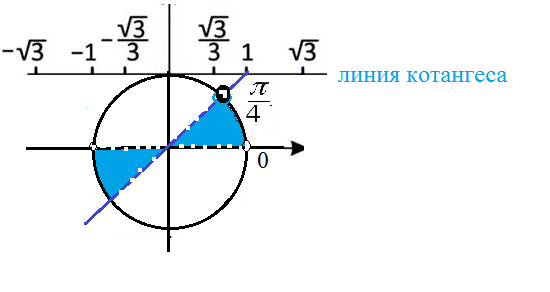
См. рис.