Задача 62065 Найдите решение неравенств (номер 21.11)...
Условие
математика 10-11 класс
600
Решение
★
2sinx < [b]sin2x[/b]*cosx
2sinx< [b]2 sinx * cosx[/b]* cosx
2sinx< 2 sinx * cos^2x
2sinx- 2 sinx * cos^2x <0
2sinx*(1-cos^2x) <0
Так как
0≤ cos^2x ≤ 1 ⇒
0 ≤ 1-cos^2x ≤ 1
Произведение двух множителей отрицательно, если множители разных знаков,
но так как второй множитель 1-cos^2x ≥ 0, то
⇒
{2sinx <0 ⇒ - π+ 2πn<x<0 +2πn, n ∈ [b]Z[/b]
{cos^2x ≠ 1 ⇒ cosx ≠ ±1 ⇒ x ≠ πk, k ∈ Z
-π+2πn<x<2πn, n ∈ [b]Z[/b]
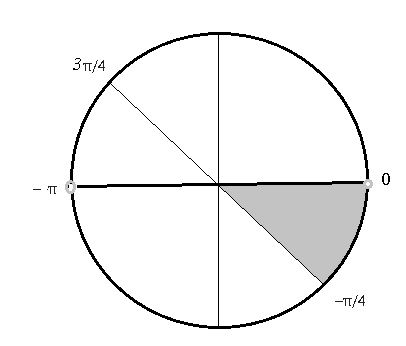
О т в е т. [-π/4; 0)
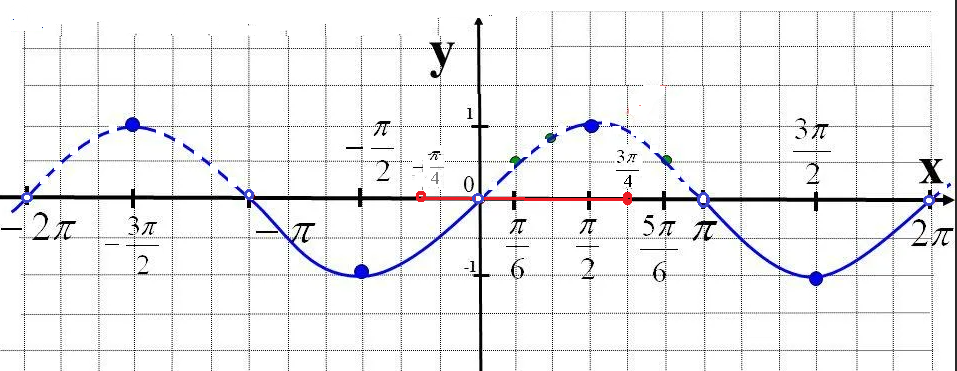
Cм на графике синуса:
части графика, расположенные ниже оси Ох изображены сплошной линией.
Надо найти пересечение таких участков с отрезком [-π/4; 3π/4]
