Задача 60732 sinx(1-2sin2x)<cos3x...

6035fc7016e9eb62f3f77539

15.09.2021 07:09:35

sinx(1-2sin2x)<cos3x

5f3ea7e3faf909182968ddd9

15.09.2021 11:11:13

★

sinx*(1-2sin2x)=sinx(1-2*2sinx*cosx)=sinx-4sin^2x*cosx=sinx- 4*(1-cos^2x)*cosx=sinx-4cosx+4cos^3x

cos3x=4cos^3x-3cosx

sinx-4cosx+4cos^3x < 4cos^3x-3cosx ⇒

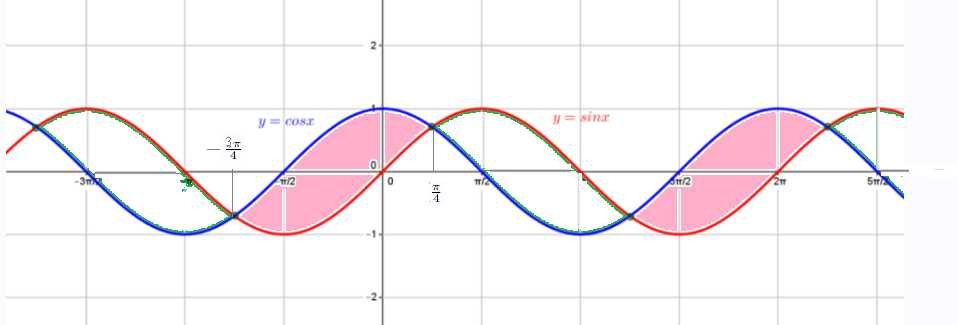
[b]sinx-cosx<0[/b]

[m](-\frac{3π}{4]+2πn;\frac{π}{4]+2πn), n ∈[/m] [b]Z [/b] - о т в е т