Задача 59895 ...
Условие
cos² πx-sin²πх≥0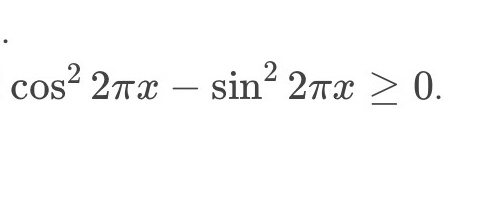
Решение
2cos^22πx ≥ 1
cos^22πx ≥ 1/2
|cos2πx| ≥ sqrt(2) /2 ⇒
cos2πx ≤ -sqrt(2) /2 [red] или [/red] cos2πx ≥ sqrt(2) /2
1)
cos2πx ≤ -sqrt(2) /2 ⇒
(3π/4)+2πn ≤ 2πx ≤ (5π/4)+2πn, n ∈ [b]Z[/b]
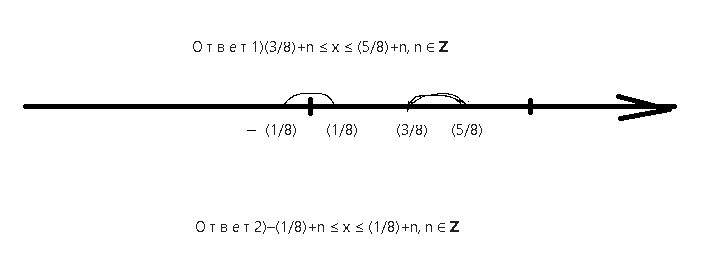
О т в е т 1)(3/8)+n ≤ x ≤ (5/8)+n, n ∈ [b]Z[/b]
[red]или[/red]
2)
cos2πx ≥ sqrt(2) /2 ⇒
-(π/4)+2πn ≤ 2πx ≤ (π/4)+2πn, n ∈ [b]Z[/b]
О т в е т 2)-(1/8)+n ≤ x ≤ (1/8)+n, n ∈ [b]Z[/b]
О т в е т. Объединение ответов 1 и 2
[-(1/8)+n;(1/8)+n] U [(3/8)+n; (5/8)+n], n ∈ [b]Z[/b]
Первый отрезок имеет длину (1/8)-(-1/8)=2/8=[b]1/4[/b]
и второй отрезок имеет длину (5/8)-(3/8)=2/8=[b]1/4[/b]
Решением неравенства являются отрезки длины (1/4)
Все решения
