Задача 59819 ...
Условие
математика 8-9 класс
643
Решение
★
8-2x=t
Решаем неравенство:
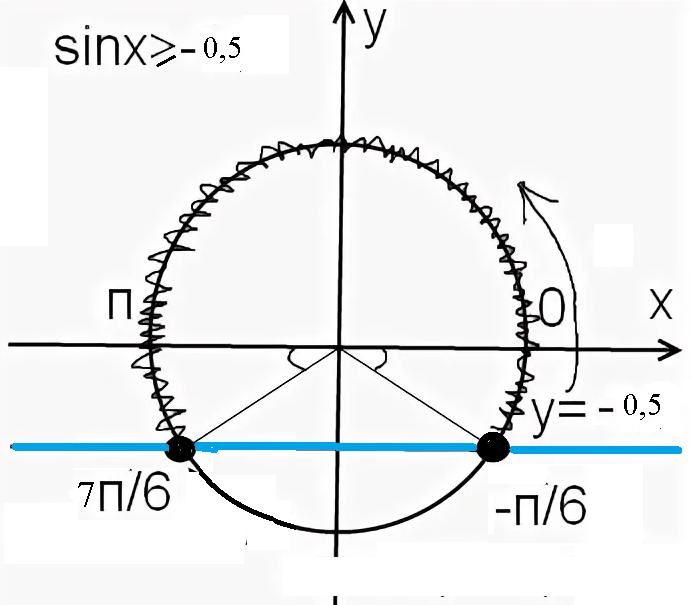
sint ≥ -0,5
( cм. рис на единичной окр.)
(-π/6)+2πn ≤ t ≤ (7π/6)+2πn, n ∈ Z
Обратный переход:
(-π/6)+2πn ≤[b] 8-2x[/b] ≤ (7π/6)+2πn, n ∈ Z
Прибавим (-8) ко всем частям:
-8+(-π/6)+2πn ≤[b] -2x[/b] ≤ -8+(7π/6)+2πn , n ∈ Z
Разделим на (-2) при этом меняем знак неравенства:
4+(π/12)-πn ≥ [b] x[/b] ≥ 4-(7π/12)-πn , n ∈ Z
Запишем в привычном виде двойного неравенства:
4-(7π/12)-πn ≤ [b] x[/b] ≤ 4+(π/12)-πn , n ∈ Z
Можно обозначить:
-n=k
4-(7π/12)+πk ≤ [b] x[/b] ≤ 4+(π/12)+πk , k ∈ Z
О т в е т. 4-(7π/12)+πk ≤ [b] x[/b] ≤ 4+(π/12)+πk , k ∈ Z