Задача 63430 Решить неравенства: буду очень...
Условие

Решение
неравенство можно записать
[m]sin2x < \frac{\sqrt{3}}{2}[/m]
это простейшее неравенство вида
[m] sint < \frac{\sqrt{3}}{2}[/m],
[m] t=2x[/m]
его решение на единичной окружности:
[m]- π-arcsin \frac{\sqrt{3}}{2}+2πn < t < arcsin \frac{\sqrt{3}}{2}+2πn, n ∈ [/m] [b]Z[/b]
так как [m] arcsin \frac{\sqrt{3}}{2}= \frac{π}{3}[/m]
получаем:
[m]- π-\frac{π}{3}+2πn < t < \frac{π}{3}+2πn, n ∈ [/m] [b]Z[/b]
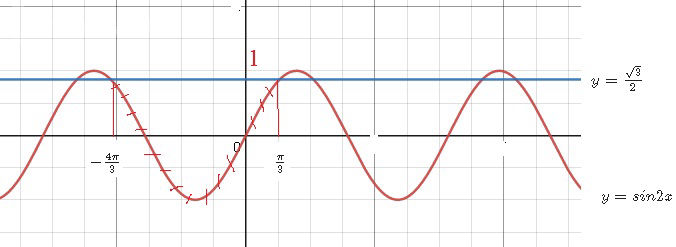
На графике: та часть [m]y=sin2x [/m] расположенная ниже прямой [m]y=\frac{\sqrt{3}}{2}[/m] заштрихована
Берется участок, расположенный ближе к нулю.
Отмечены значения [m] -\frac{4π}{3}[/m] и [m] \frac{π}{3} [/m]
Обратный переход от переменной к t к переменной х:
[m]-\frac{4π}{3}+2πn < 2x< \frac{π}{3}+2πn, n ∈ [/m] [b]Z[/b]
Делим на 2
[red][m]-\frac{2π}{3}+πn < x< \frac{π}{6}+πn, n ∈ [/m] [b]Z[/b][/red] - о т в е т
==============================
Остальные неравенства разместите еще раз. Каждое неравенство в одном вопросе.
Потому что рисунки размещаются подряд, а не под каждой задачей отдельно. Устала отвечать на вопросы , какой рисунок к какому неравенству относится....