О категории
Вариант от 15 февраля 2020 года.
Практика (19)
Некоторое число уменьшили на 20%. На сколько процентов надо увеличить результат, чтобы получить первоначальное число? [Ларин1]
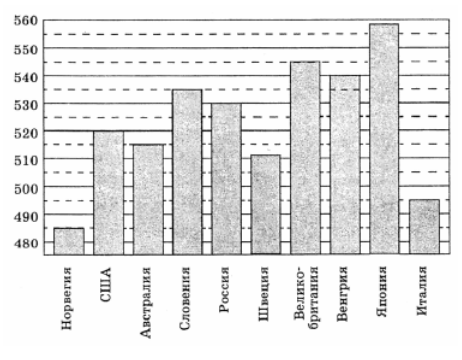
На диаграмме показан средний балл участников 10 стран в тестировании учащихся 8-го класса по обществознанию в 2007 году (по 1000-бальной шкале). По данным диаграммы найдите число стран, в которых средний балл участников не меньше, чем 515.
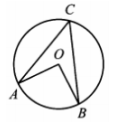
Центральный угол на 36 ° больше острого вписанного угла, опирающегося на ту же дугу окружности. Найдите вписанный угол. Ответ дайте в градусах. [Ларин 3]
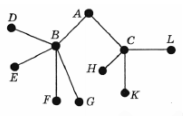
Пенсионер гуляет по дорожкам парка. На каждой развилке он наудачу выбирает следующую дорожку, не возвращаясь обратно. Схема дорожек показана на рисунке. Пенсионер начинает прогулку в точке А. Найдите вероятность того, что он придет в точку G.
Решите уравнение
log(1/8)x+5log4x+log(sqrt(2))x = 16 целых 2/3
Найдите площадь равнобедренной трапеции, если ее диагональ, равная 10, образует с основанием угол, косинус которого равен sqrt(2)/10 [Ларин 6]
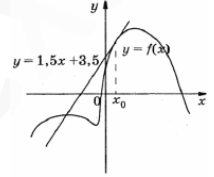
На рисунке изображен график функции у = f(x) и касательная к этому графику, проведенная в точке x_0 . Уравнение касательной дано на рисунке. Найдите значение производной функции у = 2f(x)-1 в точке x_0
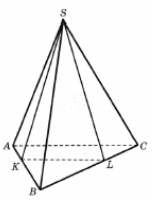
В правильной треугольной пирамиде SABC ребра ВА и ВС разделены точками K и L так, что ВК=BL=4 и KA=LC=2. Найдите угол между плоскостью основания АВС и плоскостью сечения SKL. Ответ выразите в градусах. [ларин 8]
Найдите значение выражения
sqrt(|40sqrt(2)-57|) - sqrt(40sqrt(2)+57)
Автомобиль разгоняется с места с постоянным ускорением а = 0,2 м/с^2 и через некоторое время достигает скорости v = 7 м/с. Какое расстояние к этому моменту прошел автомобиль? Ответ выразите в метрах. Скорость v, пройденный путь l, время разгона t и ускорение a связаны соотношениями v = at; l = at^2/2
Из города в деревню одновременно отправились бегун Б и пешеход П1 , а в тот же момент из деревни в город вышел пешеход П2 . Скорости пешеходов были равны. Встретившись, Б и П2 некоторое время стояли на месте, а затем направились в деревню. При этом Б побежал с прежней скоростью, равной 12 км/ч, а П2 уменьшил свою скорость в полтора раза. В результате в деревню сначала прибежал Б, а затем через промежуток времени, в два раза больший длительности встречи Б и П2 , одновременно пришли оба пешехода. Найти скорость пешехода П1
Найдите наименьшее значение функции [m]у = \frac{x^3+x^2+9}{x}-x^2[/m] на отрезке [1;10]
а) Решите уравнение
log(3+2x-x^2)((sinx+sqrt(3)cosx)/(sin3x)) = 1/log2(3+2x-x^2)
б) Укажите корни этого уравнения, принадлежащие отрезку [Pi/2; 5Pi/4]
Дан куб ABCDA_1B_1C_1D_1 с ребром длины 1. Точка P - середина A_1D_1, точка Q делит отрезок АВ_1 в отношении 2:1, считая от вершины А, R - точка пересечения отрезков ВС_1 и В_1С.
а) Найдите площадь сечения куба плоскостью PQR
б) Найдите отношение, в котором плоскость сечения делит диагональ АС_1 куба.
Решите неравенство:
[m]\frac{14^x}{7(log_7(x-3)^2)^4*log_6(x+2)} ≤ \frac{(4*2^x)^x}{4(log_7(x-3)^2)^4*log_6(x+2)}[/m]
Окружность радиуса sqrt(3) касается прямой а в точке А, а прямой b в точке В так, что хорда АВ стягивает дугу окружности в 60 ° . Прямые а и b пересекаются в точке F. Точка С расположена на луче FA, а точка D - на луче BF так, что AC=BD=2.
а) Докажите, что треугольник BAD - прямоугольный
б) Найдите длину медианы треугольника CBD, проведенную из вершины D.
В контейнер упакованы комплектующие изделия трех типов. Стоимость и вес изделия составляют 400 тыс.руб. и 12 кг для первого типа, 500 тыс.руб. и 16 кг для второго типа, 600 тыс.руб. и 15 кг для третьего типа. Общий вес комплектующих равен 326 кг. Определить минимальную и максимальную возможную суммарную стоимость находящихся в контейнере комплектующих изделий.
Найдите все значения параметра а, при каждом из которых уравнение
[m]\sqrt{3a+\sqrt{3a+2x-x^2}} = 2x-x^2[/m]
имеет решения.
Множество А состоит из натуральных чисел. Количество чисел в А больше семи. Наименьшее общее кратное всех чисел в А равно q и никакие два числа в множестве А не являются взаимно простыми. Найдите все числа множества А, если:
а) q = 210, произведение всех чисел из А делится на 1920 и не является квадратом никакого целого числа.
б) q = 390, произведение всех чисел из А не делится на 160 и не является четвертой степенью никакого целого числа.
в) q = 330, произведение всех чисел из А не является четвертой степенью никакого целого числа, а сумма всех чисел из А равна 755.




