О категории
Практика (19)
Летом килограмм клубники стоит 60 рублей. Маша купила 3 кг 800 г клубники. Сколько рублей сдачи она должна была получить с 250 рублей?
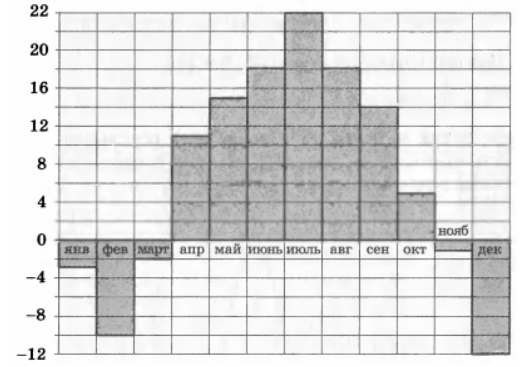
На диаграмме показана средняя температура в Самаре за каждый месяц 2001 года. По горизонтали указываются месяцы, по вертикали - температура в градусах Цельсия. Определите по приведенной диаграмме, сколько в 2001 году было месяцев с положительной средней температурой. Ответ дайте в градусах Цельсия.
На клетчатой бумаге изображены два круга. Площадь внутреннего круга равна 5. Найдите площадь закрашенной фигуры.

Вероятность того, что планшет выйдет из строя в течение первого года работы, равна 0,2. Если планшет проработал какое-то время, то вероятность его поломки в течение следующего года такая же (планшет не содержит изнашивающихся деталей, поэтому вероятность его поломки не растет со временем). Найдите вероятность, что такой новый планшет выйдет из строя не позже чем через два года после покупки.
Решите уравнение sqrt(x+4)+x-2 = 0 . Если уравнение имеет более одного корня, в ответе укажите больший из них.
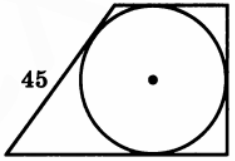
Периметр прямоугольной трапеции, описанной около окружности, равен 100, ее большая боковая сторона равна 45. Найдите радиус окружности.
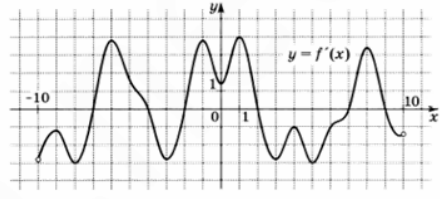
На рисунке изображен график y = f'(x) - производной функции f (x), определенной на интервале (—10; 10). Найдите количество точек максимума функции f(x) , принадлежащих отрезку [—9;8]
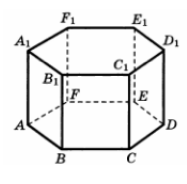
В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 площадь основания равна 13, а боковое ребро равно 12. Найдите объем призмы ACDFA1C1D1F1.
Найдите значение выражения [m]((\sqrt[4]{3}-\sqrt[4]{27})^2+7)((\sqrt[4]{3}+\sqrt[4]{27})^2-7)[/m]
Небольшой мячик бросают под острым углом а к плоской горизонтальной поверхности земли. Максимальная высота мячика, выраженная в метрах, определяется формулой [m]H = \frac{v_0^2}{4g}(1-cos2 α )[/m], где v0 = 20 м/с - начальная скорость мячика, а g - ускорение свободного падения (считайте g = 10 м/с^2). При каком значении угла α (в градусах) мячик пролетит над стеной высотой 4 м на расстоянии 1 м?
Расстояние в 180 км между пунктами А и Б автомобиль проехал со средней скоростью 40 км/ч. Часть пути по ровной дороге он ехал со скоростью 80 км/ч, а другую часть, по бездорожью, со скоростью 20 км/ч. Какое расстояние автомобиль проехал по ровной дороге?
Найдите наибольшее значение функции у = 14sqrt(2)sinx-14x+3,5Pi+3 на отрезке [0; Pi/2]
sin(Pi-x)-cos(Pi/2+x)=-1, [-Pi, 3Pi/2]
Ларин 13
В правильной треугольной призме АВСА1В1С1 сторона AB основания равна 6, а боковое ребро АА1 равно 3. На ребрах AB и В1С1 отмечены точки K и L соответственно, причём АК=В1L= 2. Точка M - середина ребра A1C1. Плоскость γ параллельна прямой AC и содержит точки K и L.
а) Докажите, что прямая BM перпендикулярна плоскости γ .
б) Найдите объём пирамиды, вершина которой - точка M, а основание - сечение данной призмы плоскостью γ .
Ларин 14
log3(x+[m]\frac{1}{x}[/m]) - 2log9(x-1) ≤ log3(3x+4) - log(27)x^6
Ларин 15
Две окружности пересекаются в точках А и В. Через точку В проведена прямая, пересекающая окружности в точках С и D, лежащих по разные стороны от прямой АВ. Касательные к этим окружностям в точках С и D пересекаются в точке Е.
а) Докажите, что вокруг четырехугольника ACED можно описать окружность
б) Найдите АЕ, если АВ=10, АС=16, AD=15.
Ларин 16
В июле 2019 года планируется взять кредит на 1 000 000 рублей. Условия возврата таковы:
- каждый январь долг возрастает на 5% по сравнению с концом предыдущего года
- с февраля по июнь каждого года необходимо выплатить часть долга;
- в 2020, 2022, 2024, 2026 годах надо выплатить 100 000 рублей;
- в остальные годы необходимо выплатить суммы, отличающиеся друг от друга на 50 000 рублей (в 2021 самая крупная выплата, в 2023 - на 50 000 рублей меньше и т.д.)
- в июле 2027 года сумма долга должна равняться нулю.
Какую сумму необходимо выплатить банку в течение всего срока кредитования?
Ларин 17
Найдите все значения параметра a, при каждом из которых неравенство
a(1+(4-sinx)^4) > 3-cos^2x
выполнено при любом значении x
Имеется несколько камней, массы которых - различные натуральные числа
а) Можно ли разложить 10 камней с массами 1,2,3...,10 по 6-ти кучкам, чтобы вес каждой кучки не превосходил 10?
б) Можно ли разложить камни массами 370,372,374.468 на семь кучек, чтобы вес каждой кучки не превосходил 3000?
в) Дополнительно известно, что общая сумма масс камней равна 4000, а масса каждой кучки, как и каждого камня не превосходит 100. Какое минимальное количество таких кучек придется задействовать, чтобы гарантированно распределить данные камни.
Ларин 19




