О категории
Вариант от 8 февраля 2020
Практика (16)
С двух полей, первое из которых по площади вдвое меньше второго, собрали урожай свёклы. Средняя урожайность составила 150 ц/га, в то время, как на первом поле собрали по 156 ц/га. Какова урожайность свёклы на втором поле? [Ларин 1]
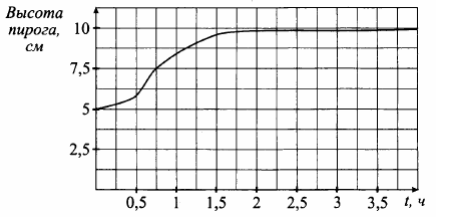
На рисунке показан график зависимости высоты пирога от времени его нахождения в духовке. По горизонтальной оси откладывается время в часах, по вертикальной - высота в см. Пока пирог не поднимется хотя бы в 1,5 раза, духовку открывать нельзя. Определите по графику, через какое минимальное время можно будет открыть духовку. Ответ дайте в часах.
Из полной колоды карт (52 листа) вынимают сразу две карты. Одну из них смотрят - она оказалась дамой. После этого две вынутые карты перемешивают и одну из них берут наугад. Найти вероятность того, что она окажется тузом. Результат округлите до сотых.
Решите уравнение log(sin(Pi/4)) (x+2) = 4
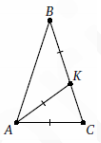
На боковой стороне CB равнобедренного (AB=BC) треугольника ABC выбрана точка K. Оказалось, что CA=AK =KB. Найдите ∠ABC. Ответ дайте в градусах. [Ларин 6]
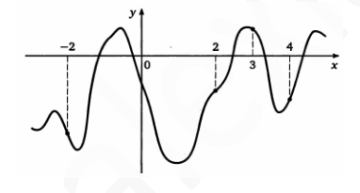
На рисунке изображен график функции y = f (x). На оси абсцисс отмечены точки -2;2;3;4. В какой из этих точек значение производной наибольшее? В ответе укажите эту точку.
Цилиндрическая кастрюля, диаметр дна которой равен 30 см, наполнена водой. Какое минимальное число кастрюль той же высоты и с диаметром дна, равным 15 см, потребуется для того, чтобы перелить в них эту воду?
Три автоматические линии выпускают одинаковую продукцию, но имеют разную производительность. Производительность всех трёх одновременно действующих линий в 1,5 раза выше производительности первой и второй линий, работающих одновременно. Сменное задание для первой линии вторая и третья линии, работая одновременно, могут выполнить на 4 ч 48 мин быстрее, чем его выполняет первая линия; это же задание вторая линия выполняет на 2 ч быстрее по сравнению с первой линией. Найти время выполнения первой линией своего сменного задания.
Найдите наименьшее значение функции
f(x) = (x-2)(x-1)(x+1)(x+2)
на отрезке [-1; 2].
а) Решите уравнение sqrt(sin((Pi/4)+x)cos((Pi/4)-x))*cosx = 1/(2sqrt(2))
б) Укажите корни этого уравнения, принадлежащие отрезку [-Pi/4; Pi]
Основанием пирамиды SABCD является прямоугольник ABCD, в котором ВС=2АВ. Диагонали прямоугольника ABCD пересекаются в точке О. Отрезок SO является высотой пирамиды SABCD. Из вершин А и С опущены перпендикуляры АР и CQ на ребро SB.
а) Докажите, что BP:PQ=1:3
б) Найдите двугранный угол пирамиды при ребре SB, если SB=BC.
Решите неравенство
[block](log(0,2)(x-2))/((4^x-8)(|x|-5)) ≥ 0[/block]
Окружность с центром на диагонали АС трапеции ABCD (BC || AD) проходит через вершины А и В, касается стороны CD в точке С и пересекает основание AD в точке E так, что CD = 6sqrt(13), AE = 8.
а) Найдите площадь трапеции ABCD
б) Прямые CD и BE пересекаются в точке Q. Найдите BQ.
Завод закупает станки двух типов, на приобретение которых выделено 34 млн. рублей. Станок первого типа занимает площадь 7 м^2 (с учетом проходов), производит за смену 5000 единиц продукции и стоит 4 млн. рублей. Станок второго типа занимает площадь 4 м^2 (с учетом проходов), производит за смену 3000 единиц продукции и стоит 3 млн. рублей. Станки должны быть размещены на площади, не превышающей 50 м^2. Сколько станков каждого типа нужно приобрести, чтобы производить за смену наибольшее количество продукции?
Найдите все значения параметра a, при каждом из которых система уравнений
{ y=a(x-3)
{ 1/log(x)2 + 1/log(y)2 = 1
не имеет решений.
Имеется 2 млн. рублей, которые надо полностью истратить на покупку путевок в дома отдыха. Путевки есть на 15, 27 и 45 дней. Стоимость их соответственно 21 тыс. руб., 40 тыс. руб. и 60 тыс. руб.
а) Можно ли купить 15 путевок первого типа?
б) Какое наименьшее возможно число путевок второго типа можно купить?
в) Сколько и каких путевок надо купить, чтобы сделать число дней отдыха наибольшим?


