О категории
Практика (19)
Для приготовления вишнёвого варенья на 1 кг вишни нужно 1,5 кг сахара. Какое наименьшее количество килограммовых упаковок сахара нужно, чтобы сварить варенье из 23 кг вишни?
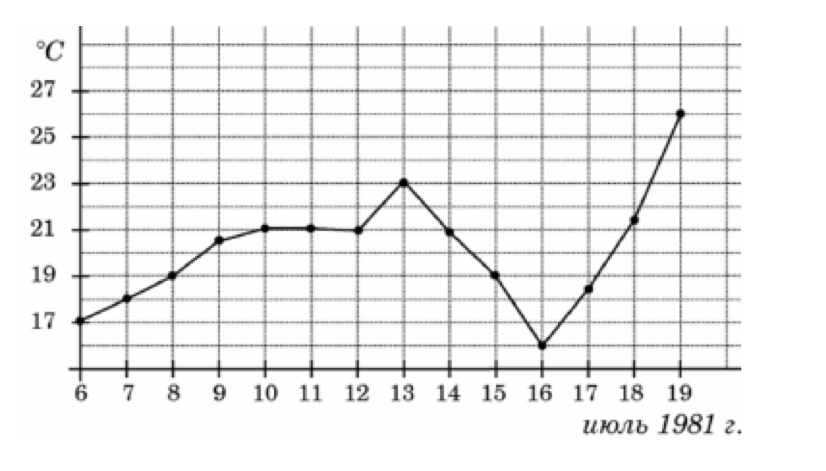
На рисунке жирными точками показана среднесуточная температура воздуха в Бресте каждый день с 6 по 19 июля 1981 года. По горизонтали указываются числа месяца, по вертикали ‐ температура в градусах Цельсия. Для наглядности жирные точки соединены линией.
Определите по рисунку, какой была наименьшая среднесуточная температура за указанный период. Ответ дайте в градусах Цельсия.
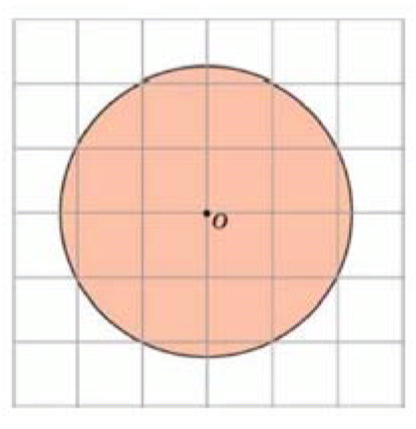
Найдите площадь S круга, считая стороны квадратных клеток равными 1. В ответе укажите S/Pi.
Механические часы с двенадцатичасовым циферблатом в какой‐то момент сломались и перестали идти. Найдите вероятность того, что часовая стрелка остановилась, достигнув отметки 7, но не дойдя до отметки 1.
Решите уравнение sqrt(x^3-4x^2+4x) = 1. В ответ укажите рациональный корень.
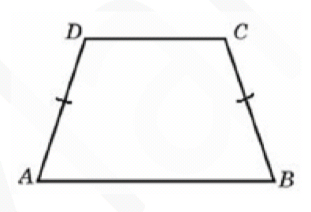
Основания равнобедренной трапеции равны 14 и 26, а ее периметр равен 60. Найдите площадь трапеции.
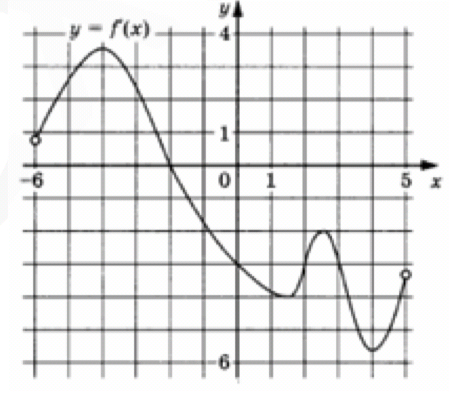
На рисунке изображен график y=f’(x) производной функции f(x), определенной на интервале ( -6 ; 5) . Найдите количество точек, в которых касательная к графику функции f (x) параллельна прямой y=-3x+7 или совпадает с ней.
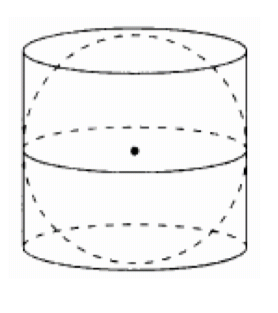
Шар, объем которого равен 72, вписан в цилиндр. Найдите объем цилиндра.
Найдите значение выражения sqrt(32)-sqrt(128)sin^2(7Pi/8)
В сейсмоопасных районах действуют специальные правила монтажа оборудования. В больнице устанавливают медицинский прибор. Корпус прибора имеет форму цилиндра радиусом R см и высотой h см. Прибор стоит на полу и может перевернуться во время землетрясения, если [m]\mu = \frac{2R}{h}[/m], где μ - коэффициент трения между корпусом прибора и полом. Если прибор может перевернуться, его нужно дополнительно прикрепить к стене. Какая наибольшая высота корпуса прибора допустима, чтобы можно было обойтись без дополнительного крепления? Радиус корпуса равен 34 см, а коэффициент трения μ равен 0,8. Ответ дайте в сантиметрах.
Пароход, отчалив от пристани А, спустился вниз по течению реки на 60 км до устья впадающего в реку притока и поднялся вверх по притоку (против течения) на 20 км до пристани В. Весь путь от А до В пароход прошёл за 7 часов. Скорость течения реки и скорость течения притока равны 1 км/ч. Найти собственную скорость парохода в км/ч. (Собственная скорость - скорость в неподвижной воде.)
Найдите наименьшее значение функции y=x^3+6x^2+9x+21 на отрезке [-3;0]
sin(Pi/3 - 2x) = -2cos^2(Pi/12 + x)-1, [Pi/2; 7Pi/2]
Ларин-13, 278
В правильной треугольной пирамиде SABC сторона основания AB равна 6, а боковое ребро SA равно 4. Точки M и N – середины рёбер SA и SB соответственно. Плоскость α содержит прямую MN и перпендикулярна плоскости основания пирамиды
а) Докажите, что плоскость α делит медиану CE основания в отношении 5:1, считая от точки C.
б) Найдите периметр многоугольника, являющегося сечением пирамиды SABC плоскостью α.
3^(2x^2)+3^(x^2+2x+5) ≥ 10*3^(4x+6)
Ларин - 15, 278
В четырехугольнике ABCD через каждую его вершину проведена прямая, проходящая через центр вписанной в него окружности. Три из этих прямых обладают тем свойством, что каждая из них делит площадь четырехугольника на две равновеликие части.
а) Докажите, что и четвертая прямая обладает тем же свойством.
б) Какие значения могут принимать углы этого четырехугольника, если один из них равен 108°?
В июле 2019 года планируется взять кредит в банке на 6 лет в размере 880 000 рублей. Условия его возврата таковы:
‐ каждый январь долг возрастает на 20% по сравнению с долгом на конец предыдущего года;
‐ с февраля по июнь ежегодно необходимо выплатить по 250 000 рублей;
‐ в 2024 и 2025 годах дополнительно производятся выплаты по S рублей;
‐ к июлю 2025 года долг будет выплачен полностью
Найдите S.
Ларин 17, 278
Найдите все значения параметра а , при каждом из которых уравнение
a^2ctg^2x-9а+a^2=4a*sinx
имеет хотя бы один корень.
Учащиеся 11 классов сдавали тесты по различным предметам. Каждый тест оценивается от 0 до 100 баллов. После получения результатов пятеро друзей решили сравнить полученные баллы. Каждый сдавал русский язык и профильную математику, четверо сдавали физику, трое сдавали информатику, и двое сдавали обществознание. Общая сумма баллов по физике не больше 300, а по информатике - не меньше 220. Сумма баллов по обществознанию оказалась равна сумме двух лучших результатов по физике и информатике.
а) Мог ли один из друзей не сдать хотя бы один экзамен?
б) Могли ли двое не сдать какой-то экзамен, если два участника написали обществознание на 87 и 78 баллов?
в) Какое наибольшее количество участников могли не сдать хотя бы один экзамен, если лучшая работа по физике оценена не более чем в 80 баллов, по информатике - не более 75 баллов, по обществознанию - не менее 90 баллов?
*) тест считается не сданным, если за него получено 0 баллов




