Задача 44089 Основанием пирамиды SABCD является...

slava191

2020-02-08 21:56:00

Основанием пирамиды SABCD является прямоугольник ABCD, в котором ВС=2АВ. Диагонали прямоугольника ABCD пересекаются в точке О. Отрезок SO является высотой пирамиды SABCD. Из вершин А и С опущены перпендикуляры АР и CQ на ребро SB.

а) Докажите, что BP:PQ=1:3

б) Найдите двугранный угол пирамиды при ребре SB, если SB=BC.

sova

2020-02-09 14:05:33

★

В основании пирамиды прямоугольник.
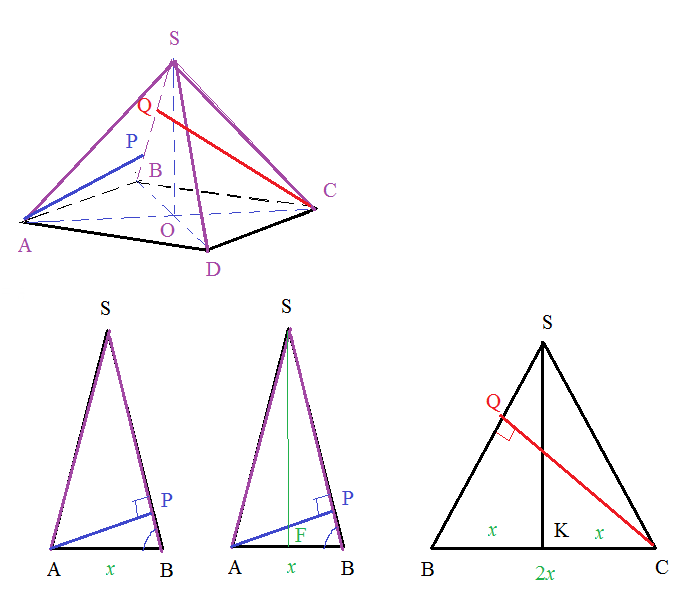
Диагонали прямоугольника [i]равны[/i] и в точке пересечения делятся [i]пополам[/i]

АО=ВО=СО=DO

SO ⊥ пл. АВСD

АО - проекция SA.

Значит SA=SB=SC=SD ( равные проекции имеют равные наклонные)

[b]a) [/b]Δ SAB - равнобедренный (SA=SB)

По условию AP ⊥ SB

Проведем SF ⊥ АВ.

Пусть АВ=x

AF=FB=x/2

Δ SFB ∼ APB ( они прямоугольные и ∠ B - общий )

Из подобия пропорциональность сторон:

ВР: AF=AB:SA ⇔ [b]BP=x^2/(2SA)[/b]

Аналогично,

Δ SBС - равнобедренный (SВ=SС)

По условию СQ ⊥ SB

Проведем SК ⊥ ВС.

Пусть ВС=2АВ=2x

ВК=КС=x

Δ SKB ∼ CQB ( они прямоугольные и ∠ B - общий )


Из подобия пропорциональность сторон:

ВQ: BK=BC:SB ⇔ [b]BQ=2x^2/(SB)[/b]

[b]SA=SB[/b]

[red]BP:BQ=1:4[/red] ⇒ BP:PQ=1:3

О т в е т. [b]a) BP:PQ=1:3[/b]

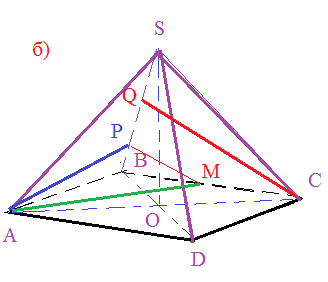
[b]б)[/b]

В треугольнике SBC проведем
PM || CQ

CQ ⊥ SB ⇒ PM ⊥ SB

∠ APM -[i] линейный угол [/i]двугранного угла при ребре SB

Найдем его из треугольника АРМ.

Для этого найдем стороны треугольника АРМ.


По условию б) SB=BC

ВС=2х, SB=2x

Δ SBC - равносторонний, высота CQ - медиана

BQ=QS=x

CQ=2xsqrt(3)/2=xsqrt(3)
(высота равностороннего треугольника со стороной а равна a*sqrt(3)/2 )

Δ ВМР ∼ ВQC (PM || CQ)

BP: BQ=BM:BC

[red]BP:BQ=1:4[/red] ⇒ BM[/b]=BC/4=x/2


[b]PM[/b]=CQ/4=[b]xsqrt(3)/4[/b]


Из прямоугольного Δ АВМ:

АМ^2=AB^2+BM^2=x^2+(x^2/4)=5x^2/4

[b]AM=x*sqrt(5)/2[/b]


Из прямоугольного Δ АРВ ( АВ=х; BP=(1/4)BQ=x/4)

АР^2=AB^2-BP^2=x^2-(x/4)^2=15x^2/16

[b]AP=xsqrt(15)/4[/b]



Итак, по теореме косинусов из Δ АРМ

сos ∠ APM=(AP^2+PM^2-AM^2)/(2*AP*PM)

AP=xsqrt(15)/4

PM=xsqrt(3)/4

AM=x*sqrt(5)/2

сos ∠ APM=-sqrt(5)/15


[b]∠ APM=arccos(-sqrt(5)/15)[/b]