Задача 44289 Окружность радиуса sqrt(3) касается...

slava191

2020-02-15 17:58:13

Окружность радиуса sqrt(3) касается прямой а в точке А, а прямой b в точке В так, что хорда АВ стягивает дугу окружности в 60 ° . Прямые а и b пересекаются в точке F. Точка С расположена на луче FA, а точка D - на луче BF так, что AC=BD=2.

а) Докажите, что треугольник BAD - прямоугольный

б) Найдите длину медианы треугольника CBD, проведенную из вершины D.

sova

2020-02-15 23:38:49

★

а)
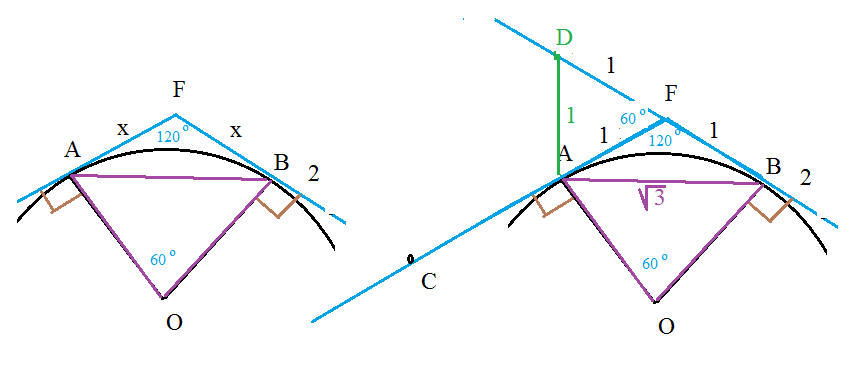
По условию ∪ AB=60 ° ⇒ центральный угол АОВ=60 °

Δ АОВ - равнобедренный ( АО=ОВ) c ∠ АОВ=60 ° при вершине,значит Δ АОВ - равносторонний
АО=ОВ=АВ=R=sqrt(3)


Касательная перпендикулярна радиусу, проведенному в точку касания.

∠ FAO= ∠ FBO=90 °

Сумма углов четырехугольника FAOB равна 360 °

Значит, ∠ АFB=120 °

По свойству касательных проведенных к окружности из одной точки
FA=FB
Пусть FA=FB=x

По теореме косинусов из Δ FAB:
АВ^2=FA^2+FB^2-2*FA*FB*cos120 °

(sqrt(3))^2=x^2+x^2-2*x*x*(-1/2) ⇒ 3=3x^2⇒ x^2=1 ⇒ x=1

(x=-1 не удовл смыслу задачи)


Так как AC=BD=2 и FA=FB=1
⇒ FС=FA+AC=1+2=3

BD=BF+FD ⇒ FD=1

Треугольник Δ FAD- равносторонний,

АD=1

В треугольнике BAD:

AB^2+AD^2=BD^2

(sqrt(3))^2+1^2=2^2

По теореме, обратной теореме Пифагора, треугольник ВАD - прямоугольный

б)
По теореме косинусов из Δ FCD:

FD^2=1^2+3^2-2*1*3*(1/2)
FD^2=7
FD=sqrt(7)

По теореме косинусов из Δ FВC:

FВ^2=1^2+3^2-2*1*3*(-1/2)
FD^2=13
FD=sqrt(13)

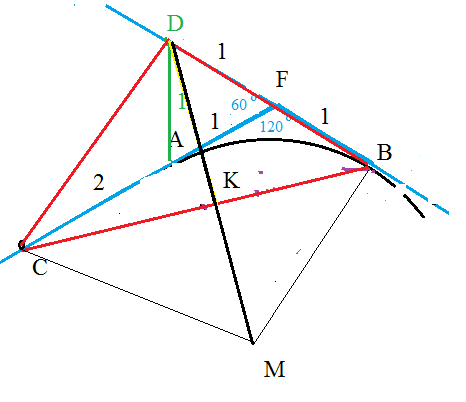
Пусть медиана DK=m

Достроим треугольник BCD до параллелограмма

MCDB

Диагональ DM=2DK=2m


По свойству диагоналей и сторон параллелограмма:

2(a^2+b^2)=d^2_(1)+d^2_(2)

2*((sqrt(7))^2+2^2)=(2m)^2+(sqrt(13))^2

4m^2=9

m=3/2

О т в е т. б) 3/2=1,5