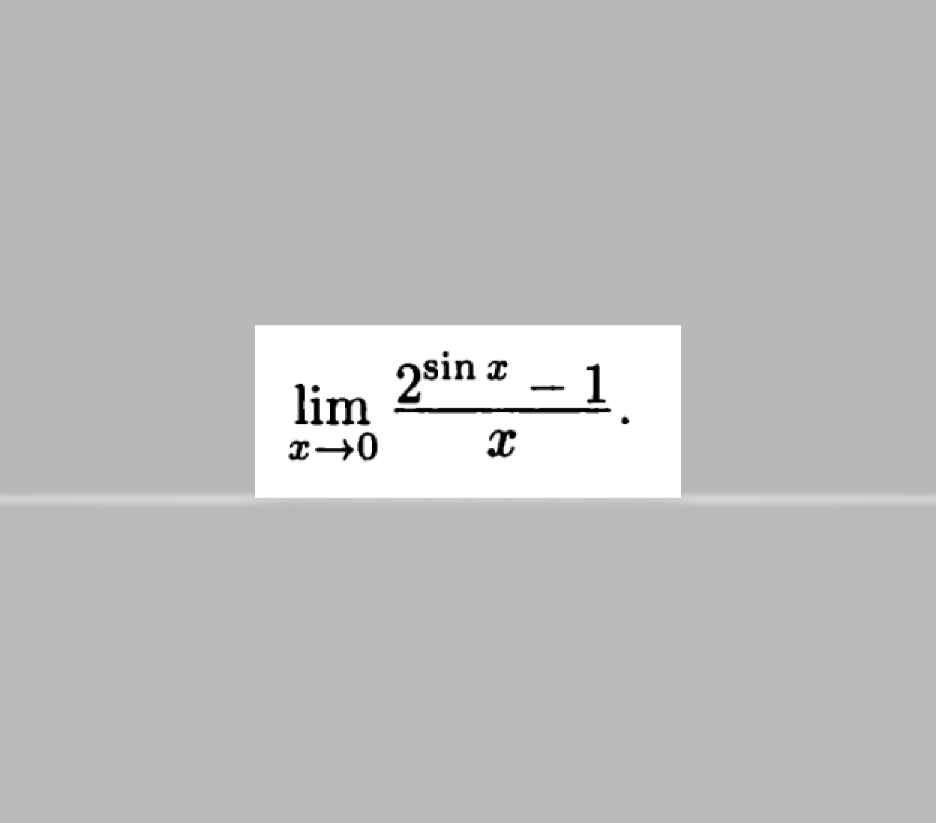
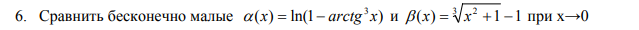Бесконечно малые

Здравствуйте, решите предел!

Вычислить предел lim_x – > π...

Вычислить предел lim_x –> 1

Пусть {x_n} — бесконечно малая, а {y_n} и {z_n} — бесконечно большие последовательности. Верно ли, что всегда:
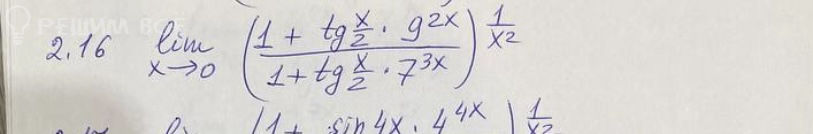
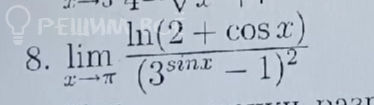
1) {x_n · y_n} — бесконечно большая последовательность;
2) {x_n · y_n} — бесконечно малая последовательность;
3) {x_n · y_n} — сходящаяся последовательность;
4) {y_n · z_n} — бесконечно большая последовательность;
5) {y_n + z_n} — расходящаяся последовательность?

e) lim x->∞ (1 - cos 4x) / (x sin x)

5. Определить характер функций f_1(x), f_2(x), f_3(x) в точке x_0 и выделить главные части.
...

6. Исследовать функции f_1(x) и f_2(x) на непрерывность, установить тип точек разрыва и построить графики функций в окрестности точек разрыва.

...

Сравнить бесконечно малые

Определить порядок малости бесконечно малых функций y(x) относительно x

Найти пределы, заменяя бесконечно малые эквивалентными