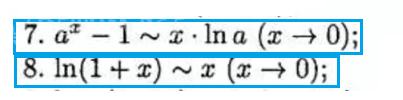Задача 67422 ...
Условие
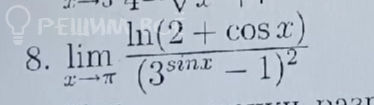
математика ВУЗ
287
Решение
★
[/red]
[m]x-π=t[/m] ⇒ [m]x=t+π[/m]
[m]x → π[/m] ⇒ [m]t → 0[/m]
[m]ln(2+cosx)=ln(2+cos(t+π)=ln(2-cost)[/m]
[m]ln(2-cost)=ln(1+(1-cost)) ∼ 1-cost[/m] при [m]t → 0[/m]
[m]3^{sinx}-1=3^{sin(t+π)}-1=3^{-sint}-1[/m]
[m]3^{-sint}-1 ∼ (-sint) [/m] при [m]t → 0[/m]
[m]lim_{x → π}\frac{ln(2+cosx)}{(3^{sinx}-1)^2}=lim_{t → 0}\frac{ln(2-cost)}{(3^{-sint}-1)^2}=lim_{t → 0}\frac{1-cost}{((-sint)\cdot ln3)^2}=lim_{t → 0}\frac{2sin^2\frac{x}{2}}{(-sint \cdot ln3)^2}=\frac{1}{2ln^23}[/m]