О категории
Геометрия на доказательство
Практика (11)
Окружности с центрами в точках P и Q пересекаются в точках К и L, причём точки Р и Q лежат по одну сторону от прямой KL. Докажите, что прямые PQ и KL перпендикулярны.
Дан выпуклый четырёхугольник. Докажите, что четырёхугольник с вершинами в серединах сторон данного четырёхугольника является параллелограммом.
Докажите, что отрезок, соединяющий середины оснований трапеции, делит её на две равные по площади части.
В равнобедренной трапеции ABCD с основаниями AD и ВС (AD > ВС) и боковыми сторонами АВ и CD диагональ АС является биссектрисой угла А. Докажите, что DB является биссектрисой угла D.
Высоты AA1 и BB1 остроугольного треугольника ABC пересекаются в точке E. Докажите, что углы AA1B1 и ABB1 равны
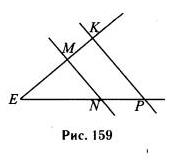
Стороны угла Е пересечены параллельными прямыми MN и КР (см. рис. 159). Докажите, что ЕМ/MK=EN/NP.
Четырёхугольник ABCD описан около окружности радиуса R. Его диагональ BD проходит через центр О этой окружности. Докажите, что MN^2 = МО^2 + NO^2, где М и N — точки касания окружности со сторонами ВС и BD, соответственно, ОВ = 2R и OD =2R/sqrt(3)
В произвольной трапеции AKND известно, что AD || KN. Точка О — точка пересечения диагоналей, точка L — точка пересечения прямых АК и ND. LO пересекает KN в точке Р, a AD — в точке М. Докажите, что AM = MD и КР = PN.
ABCD — произвольный четырёхугольник, а точки Е, F, К, N — середины его сторон, последовательно соединённые. Докажите, что полученный четырёхугольник EFKN — параллелограмм.
На средней линии трапеции ABCD с основаниями AD и ВС выбрали произвольную точку F. Докажите, что сумма площадей треугольников BFC и AFD равна половине площади трапеции.
В параллелограмме ABCD точка E — середина стороны AB. Известно, что EC = ED. Докажите, что данный параллелограмм — прямоугольник



