О категории
Геометрия. Свойства и формулы для вписанной и описанной окружностей.
Практика (10)
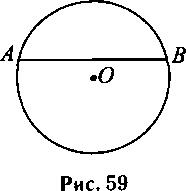
Хорда AB делит окружность с центром О на две дуги (см. рис. 59), отношение которых равно 5 : 7. Найдите величину центрального угла AOB (в градусах), опирающегося на меньшую из дуг AB.
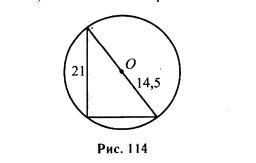
Радиус окружности, описанной около прямоугольного треугольника, равен 14,5 (см.рис.114). Один из катетов равен 21. Найдите другой катет.
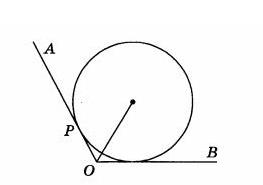
В угол АОВ величиной в 120 градусов вписана окружность, касающаяся стороны ОА в точке Р, причём ОР=1. Найдите расстояние от центра окружности до вершины этого угла.
Найдите площадь квадрата, описанного около окружности радиуса 4.
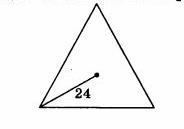
Центр равностороннего треугольника удалён от вершины треугольника на 24. Найдите радиус окружности, вписанной в этот треугольник.
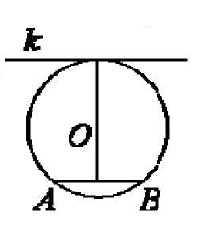
Радиус окружности с центром в точке O равен 85, длина хорды AB равна 102. Найдите расстояние от хорды АВ до параллельной ей касательной k.
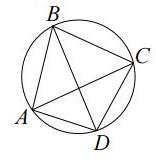
Четырехугольник ABCD вписан в окружность. Угол АВС равен 54°, угол CAD равен 41°. Найдите угол ABD. Ответ дайте в градусах.
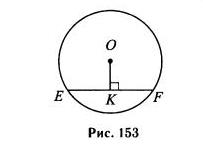
В окружности с центром в точке О проведена хорда EF (см. рис. 153). Найдите радиус окружности, если длина хорды равна 12, а расстояние от центра до хорды равно 8.
В треугольнике ABC угол C равен 90 градус, BC=15. Радиус описанной окружности этого треугольника равен 8,5. найдите AC.
Найдите длину хорды окружности радиусом 13 см, если расстояние от центра окружности до хорды равно 5 см. Ответ дайте в см.