Задача 8098 Четырехугольник ABCD вписан в...
Условие
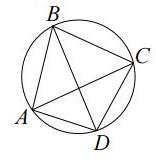
математика 8-9 класс
40095
Решение
Тогда, ∠ADC=180°-∠ABC=180°-54°=126°.
Из треугольника ADC:
∠ACD=180°-(∠CAD+∠ADC)=180°-(41°+126°)=180°-167°=13°
∠ACD - вписанный угол, который опирается на меньшую дугу AD, на эту же дугу опирается угол ABD, значит ∠ABD=∠ACD=13°
Ответ: 13
