Задача 11908 В угол АОВ величиной в 120 градусов...
Условие
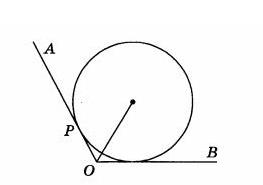
математика 8-9 класс
12882
Решение
угол СОР= 120 градусов : 2 = 60 градусов
= > угол ОСР=90 градусов - 60 градусов = 30 градусов, = > OP=1/2*OC
OC=2*OP=2*1=2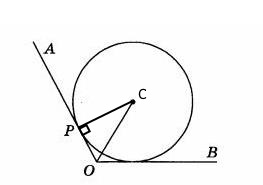
Ответ: 2
