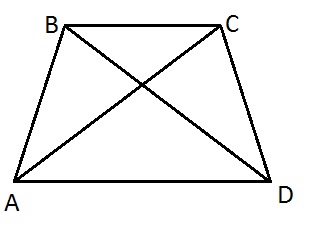
В равнобедренной трапеции ABCD с основаниями AD и ВС (AD > ВС) и боковыми сторонами АВ и CD диагональ АС является биссектрисой угла А. Докажите, что DB является биссектрисой угла D.
математика 8-9 класс
10081
AC - биссектриса угла BAD => ∠BAC=∠CAD. ∠CAD=∠BCA, т.к. внутренние накрест лежащие при параллельных прямых BC и AD и секущей AC => ∠BAC=∠BCA => треугольник АВС равнобедренный, АВ=ВС. Трапеция равнобедренная => AB=CD => BC=CD => BCD равнобедренный треугольник => ∠CBD=∠CDB как углы при основании. ∠CBD=∠BDA как внутренние накрест лежащие => ∠CDB=∠BDA => BD биссектриса угла CDA что и требовалось доказать.
Ответ: В решение

