Задача 7827 Четырёхугольник ABCD описан около...

larisashakirova

15.03.2016

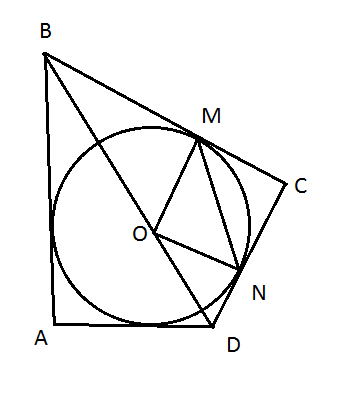
Четырёхугольник ABCD описан около окружности радиуса R. Его диагональ BD проходит через центр О этой окружности. Докажите, что MN^2 = МО^2 + NO^2, где М и N — точки касания окружности со сторонами ВС и BD, соответственно, ОВ = 2R и OD =2R/sqrt(3)

ОВ=2R, OM=R => ∠OBM=30, ∠BOM=90-30=60. OD=2R/√3, ON=R => sin∠NOD=R/(2R/√3)=√3/2 => ∠NOD = 60 => ∠MON=180-30-60=90 => треугольник MON прямоугольный => по теореме Пифагора MN^2 = МО^2 + NO^2 что и требовалось доказать.

Ответ: В решение