Задача 7458 ABCD — произвольный четырёхугольник, а...
Условие
математика 8-9 класс
6441
Решение
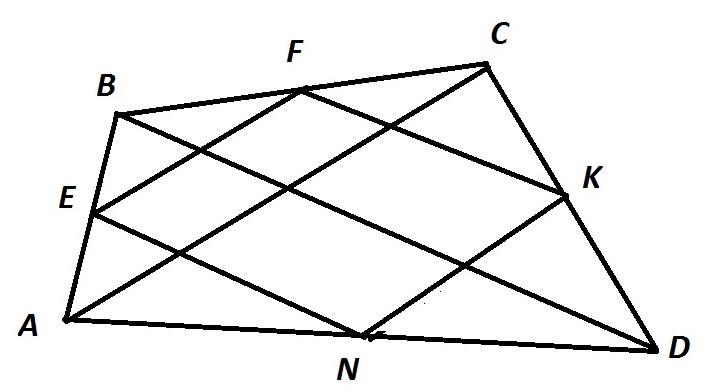
Ответ: В решение

Ответ: В решение