Задача 7566 В произвольной трапеции AKND известно,...

Julia_Trusova

08.03.2016

В произвольной трапеции AKND известно, что AD || KN. Точка О — точка пересечения диагоналей, точка L — точка пересечения прямых АК и ND. LO пересекает KN в точке Р, a AD — в точке М. Докажите, что AM = MD и КР = PN.

1. Рассмотрим △PNO и △MAO:
∠PNO=∠MAO как накрестлежащие ; ∠PON=∠MOА как вертикальные
⇒ △PNO ~ △MAO по двум углам.
Значит, PN/MA=PO/MO
2. Аналогично доказывается, что △КPO ~ △DMO
⇒ KP/DM=PO/MO
3. Значит, PO/MO=PN/MA=KP/DM
⇒ PN*DM=KP*MA
AM/MD=PN/KP
4. △КLP ~ △ALM по двум углам (∠LKP=∠LAM как соответственные, ∠KLP общий)
⇒LP/LM=KP/AM
5. Аналогично доказывается, что △NLP ~ △DLM
⇒ LP/LM=NP/DM
6. Значит, LP/LM=KP/AM=NP/DM
⇒ KP*DM=NP*AM
PN/KP=DM/AM
7. В 3 п. получили: PN/KP=AM/MD
В 6 п получили: PN/KP=DM/AM
Это возможно, только при PN/KP=AM/MD=DM/AM=1
т.е. KP=PN, AM=MD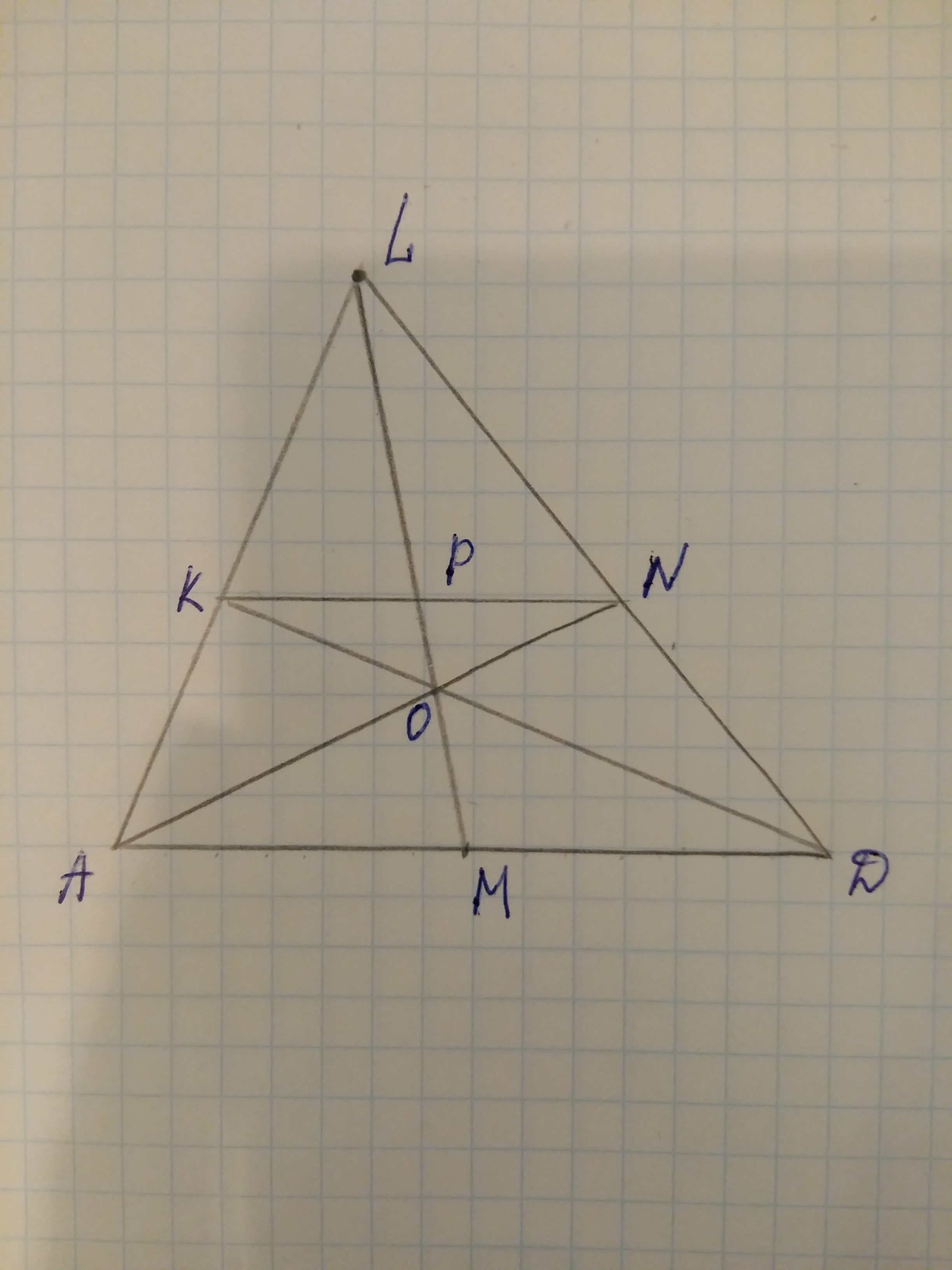

Ответ: В решение