МНОЖЕСТВА

Для универсального множества U = {–5, –4, –3, –2, –1, 1, 2, 3, 4, 5}, множества A = {–3, –1, 2, 4}, заданного списком, и для B, являющемся множеством корней уравнения x4–2x3–15x2–4x+20 = 0

1. Найти множества: A ∪ B, B ⋂ A, A \ B, B \ A, A ∆ B, B, C = (A ∆ B) ∆ A.

2. Выяснить, какая из возможностей выполнена для множества A и C: A ⊂ C, или C ⊂ A, или A = C, или A ⋂ C = ∅.

3. Найти P(B) и |P(B)|

Вариант 18 пж пж пж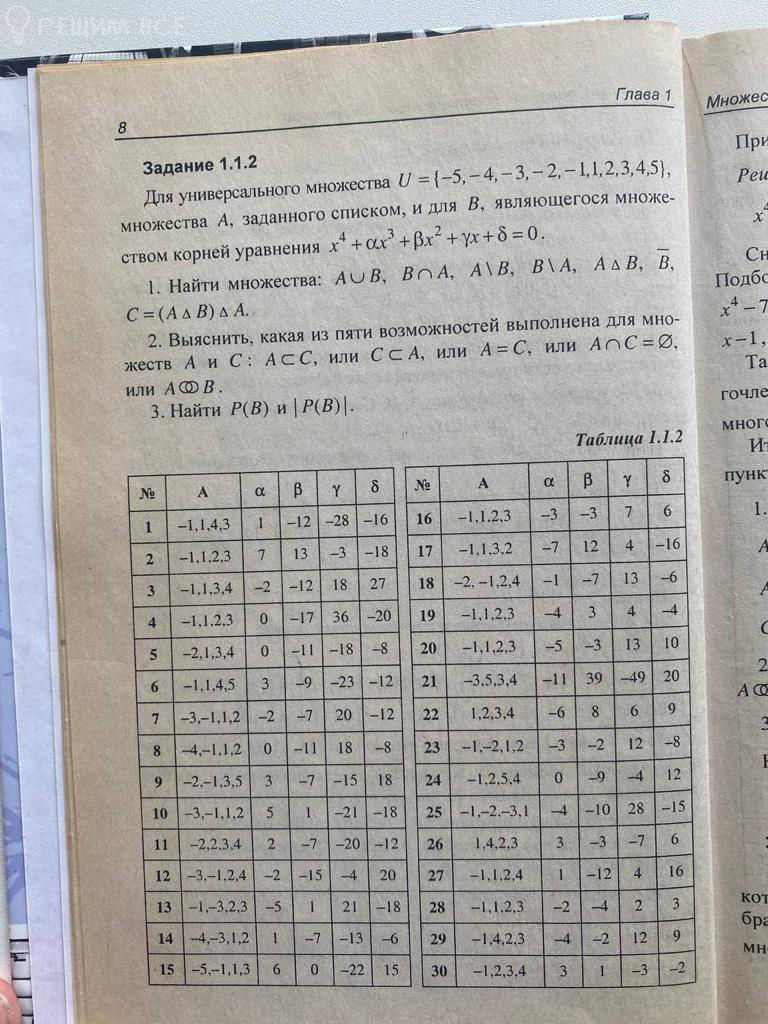

2. На паре множеств Х и У, где ... задано соответствие F. Постройте график соответствия F. Задайте соответствия F, F^–1 и F^c. Выясните свойства соответствия F.

Все вопросы 1 варианта

Пусть A, B и C — множества точек плоскости, координаты которы удовлетворяют условиям. Изобразите в системе координат xy, множество D, полученное из множество по формуле...

1. Для универсального множества U=–5, –4, –3, –2, –1, 1, 2, 3, 4, 5, множеств A=–4,–1,1,2 и B=–2,–1,1 .
1.1. Найти множества: AB, AB, A∖B, B, C=A∆B∆A.
1.2. Найти: PB, P(B).

Пусть A,В,и С — множества точек плоскости, координаты которых удовлетворяют условиям а, В и у соответственно. Изобразите в системе координат...

Для универсального множества .... множества А, заданного списком, и для B, являющегося множеством корней
уравнения ...

Найти множества:...

Для универсального множества U = {–5, –4, –3, –2, –1, 1, 2, 3, 4, 5}, множества A = {–1, 1, 2, 3}, заданного списком, и для B, являющемся множеством корней уравнения x4+7x3+13x2–3x–18 = 0

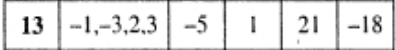
1. Найти множества: A ∪ B, B ⋂ A, A \ B, B \ A, A ∆ B, B, C = (A ∆ B) ∆ A.

2. Выяснить, какая из возможностей выполнена для множества A и C: A ⊂ C, или C ⊂ A, или A = C, или A ⋂ C = ∅.

Задание 1. Для универсального множества ... , множества... ‚ заданного списком, и для В ‚ являющегося множеством корней уравнения ...

На множестве В={3,6,9,12} заданны отношения Т и Р∶
Т ={(3,3);(6,3);(9,3);(12,3);(12,6);(6,6);(9,9);(12,12)}
Р ={(6,3);(9,6);(12,9)}
а) Постройте графы отношений.
б) Определите свойства отношений Т и Р.

Задача. Пусть даны множества A={1, 3, 7, 137}, B={3, 7, 23}, C={0, 1, 3, 23}, D={0, 7, 23, 2004}.

Найдите множества

Создатель