Задача 57074 Для универсального множества .......
Условие
уравнения ...
Найти множества:...

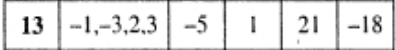
Решение
B={-2;1;3} - множество корней уравнения x^4-5x^3+x^2+21x-18=0
x^4-5x^3+x^2+21x-18=(x+2)(x-1)(x+3)^2.
A ∪ B={-1;-3;2;3}U{-2;1;3} ={–3;–2;–1;1;2;3}
A ∩ B ={-1;-3;2;[b]3[/b]} ∩ {-2;1;[b]3[/b]} ={3}
A \ B={-1;-3;2;3}U{-2;1;3}={–3;-1;2}
B \ A={-2;1;[b]3[/b]}\{-1;-3;2;[b]3[/b]}={–2;1}
A Δ B=(A \ B) U (B \ A)={–3;-1;2}U{–2;1}={–3;–2;–1;1;2}
vector{B}=U\B={–5;–4;–3;-2;-1;1;2;3;4;5}\{-2;1;3}={–5;–4;–3;-1;2;4;5}
C =(A Δ B) ΔA=((A ΔB)\A) U (A\ (A Δ B))={-2;1;3}
(A ΔB)\A={[b]–3[/b];–2;[blue][b]–1[/b][/blue];1;[b]2[/b]}\{[blue][b]-1[/b][/blue];[b]-3[/b];[b]2[/b];3}={-2;1}
A\ (A Δ B)={[blue][b]-1[/b][/blue];[b]-3[/b];[b]2[/b];3}\{[b]–3[/b];–2;[blue][b]–1[/b][/blue];1;[b]2[/b]}={3}
((A ΔB)\A) U (A\ (A Δ B))={-2;1;3}
Все решения
