Задача 66033 ...
Условие
1. Найти множества: A ∪ B, B ⋂ A, A \ B, B \ A, A ∆ B, B, C = (A ∆ B) ∆ A.
2. Выяснить, какая из возможностей выполнена для множества A и C: A ⊂ C, или C ⊂ A, или A = C, или A ⋂ C = ∅.
3. Найти P(B) и |P(B)|
Вариант 18 пж пж пж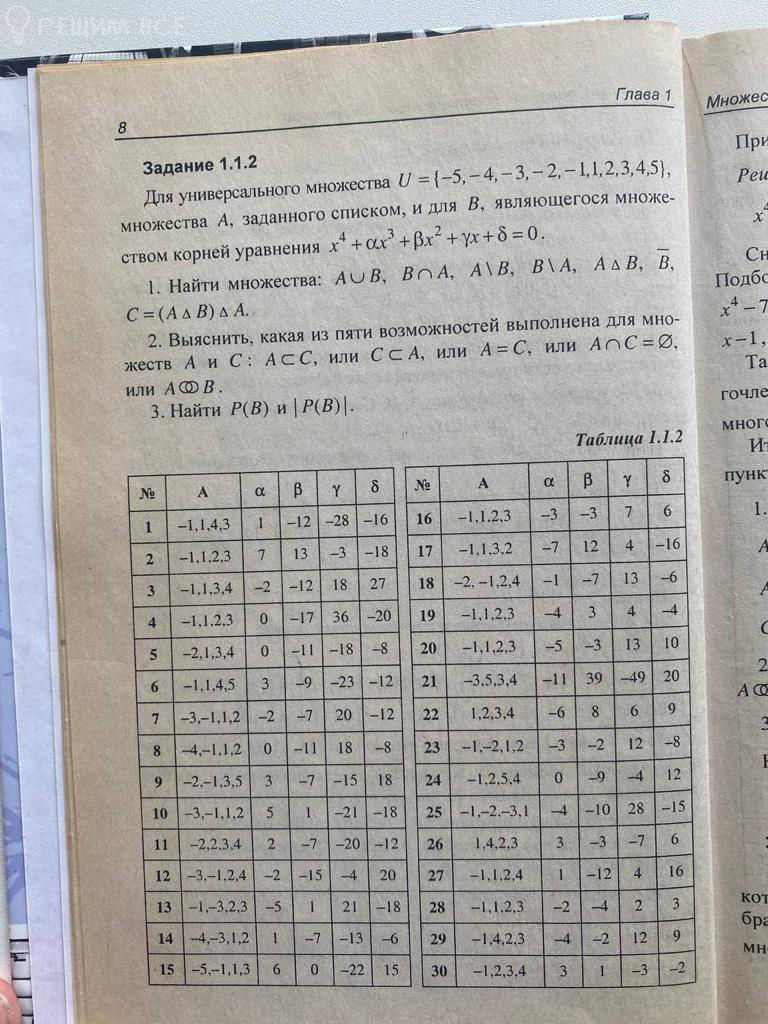
Решение
x^4-x^3-7x^2+13x–6 = 0
Решаем.
Подстановкой убеждаемся, что х=1 - корень уравнения
1-1-7+13-6=0 - верно
Значит, левая часть может быть разложена на множители:
(x-1)*(x^3-7x+6)=0
х=1 - корень уравнения x^3-7x+6=0
1-7+6=0 - верно
Значит, левая часть может быть разложена на множители:
(x-1)*(x-1)*(x^2+х-6)=0
Квадратное уравнение x^2+х-6=0 имеет корни (-2 и -3)
B={-3;-2;1}
U={-5;-4;-3;-2;-1;0;1;2;3;4;5}
A={-2;-1;2;4}
A ∪ B={-3;-2;-1;1;2;4}
A ∩ B ={-2}
A \ B={-1;2;4}
B \ A={-3;1}
A Δ B=(A \ B) U (B \ A)={-3;-1;1;2;4}
vector{B}={-5;-4;0;3;5}
C =(A Δ B) ΔA=((A ΔB)\A) U (A\ (A Δ B))=...
см решение аналогичной задачи здесь:
https://reshimvse.com/zadacha.php?id=54936