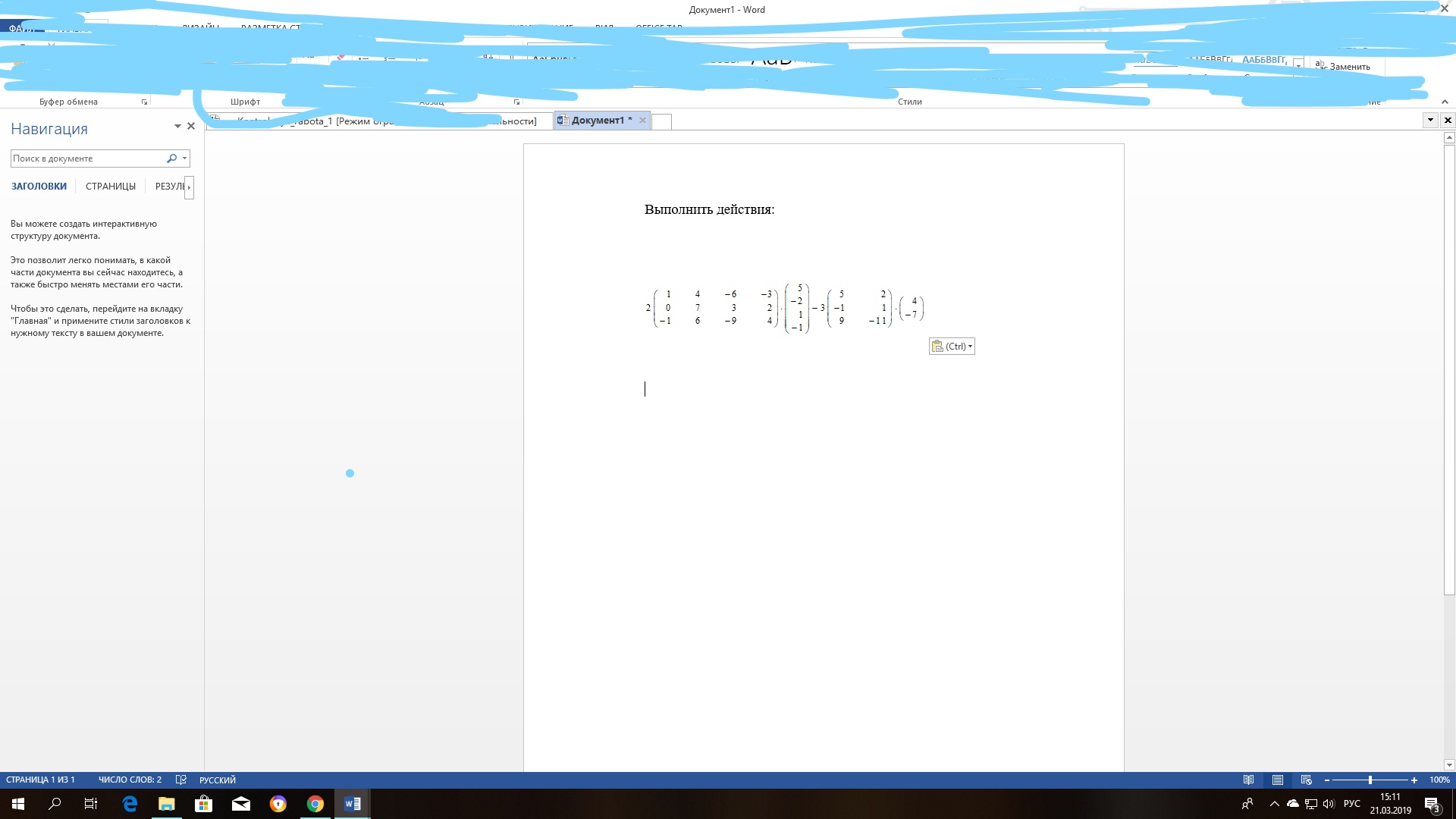
Матрицы и определители

Действия над матрицами, вычисление определитлей

Решить нужно сегодня. Решившему +10000000000 соц рейтинга от партии!! Хотя бы 4–5 пунктов

Матрица A некоторого оператора A : R3 → R3
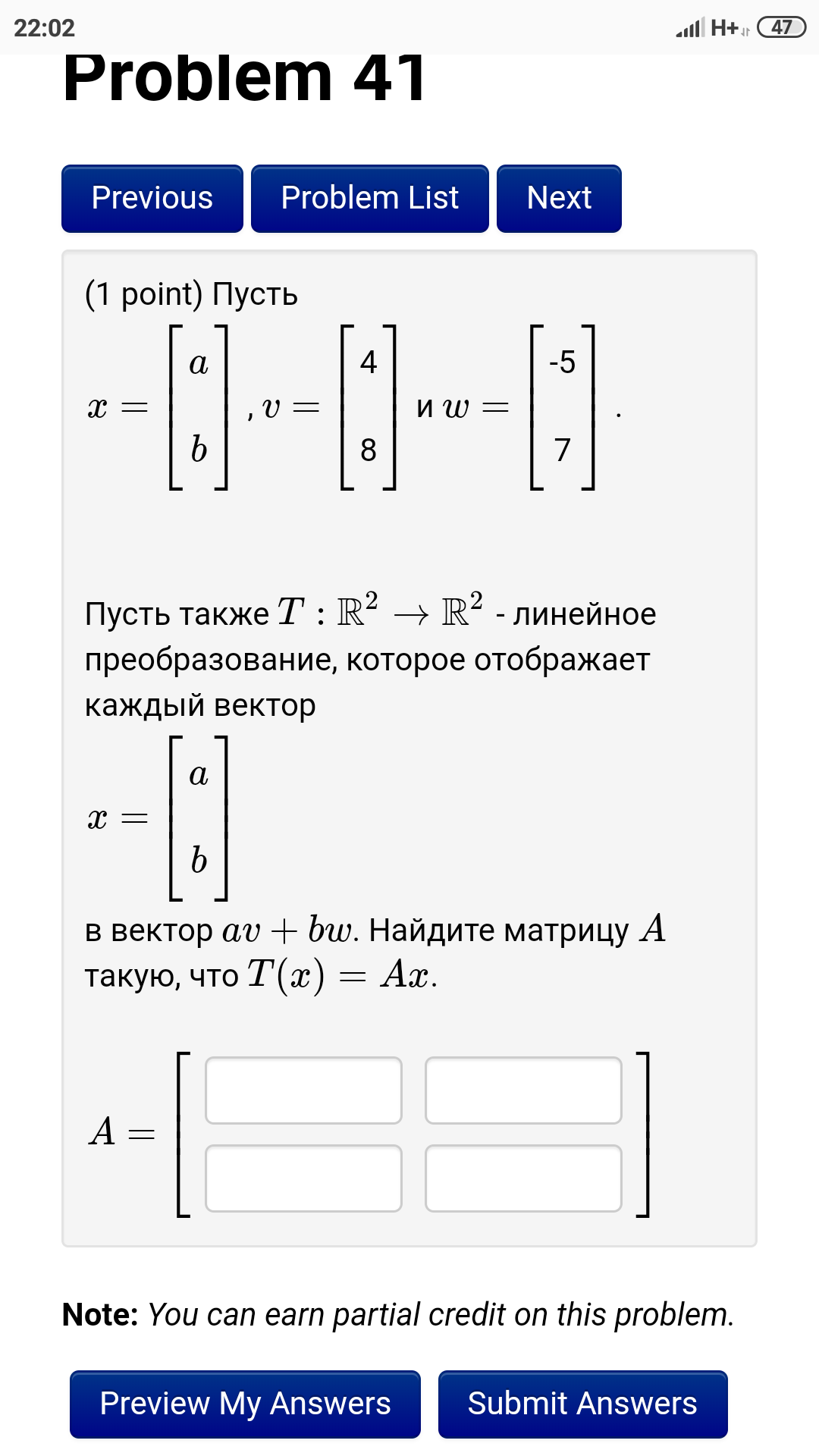
и вектор x = {0,−2, 3} заданы в базисе e1, e2, e3. Найти матрицу оператора A и образ A x вектора x в базисе f1 = e1 − e2, f2 = e1 + e2, f3 = e1 + e2 − e3.
–1 –3 0
0 –1 0
2 0 1
Ответ должен быть:
[[3/2,–1/2,–1/2,
9/2,1/2,–1/2 ,
–2,–2,1]]
[2,7,–3]

Дана система, При решении этой системы по формулам Крамера нужно вычислить определители Δ, Δx, Δy, Δz . Тогда

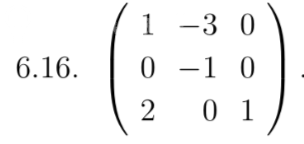
1) Δ=−12, Δx=−36, Δy=24, Δz= −12

2) Δ=−12, Δx=−36, Δy=−24, Δz= 12

3) Δ=−12, Δx=36, Δy=−24, Δz= −12

4) Δ=−12, Δx=−36, Δy=24, Δz= 12

5) Δ=1, Δx=3, Δy=–2, Δz= 1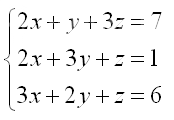

Найдите такое значение параметра λ при котором…

Доказать, что системы векторов образуют базис и найти матрицу перехода от одного базиса к другому:
e₁= (1 2 1) ; e₂= (2 3 3) ; e₃= (3 7 1)
e₁′= (3 1 4) ; e₂′ = (5 2 1) ; e₃′ = (1 1 –6)

матрицы A =
15 –11 5
20 –15 8
8 –7 6
e₁′= (3 1 4) ; e₂′= (5 2 1) ; e₃′= (1 1 –6)

Найти матрицу в базисе, где если она задана в базисе ...

Дана матрица
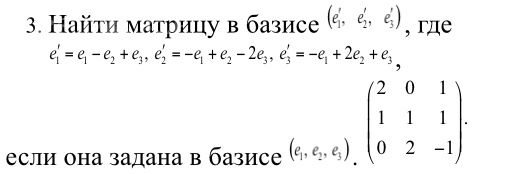
A =
[−6 −2 −2]
[ 2 −2 −10]
[−2 −6 2]
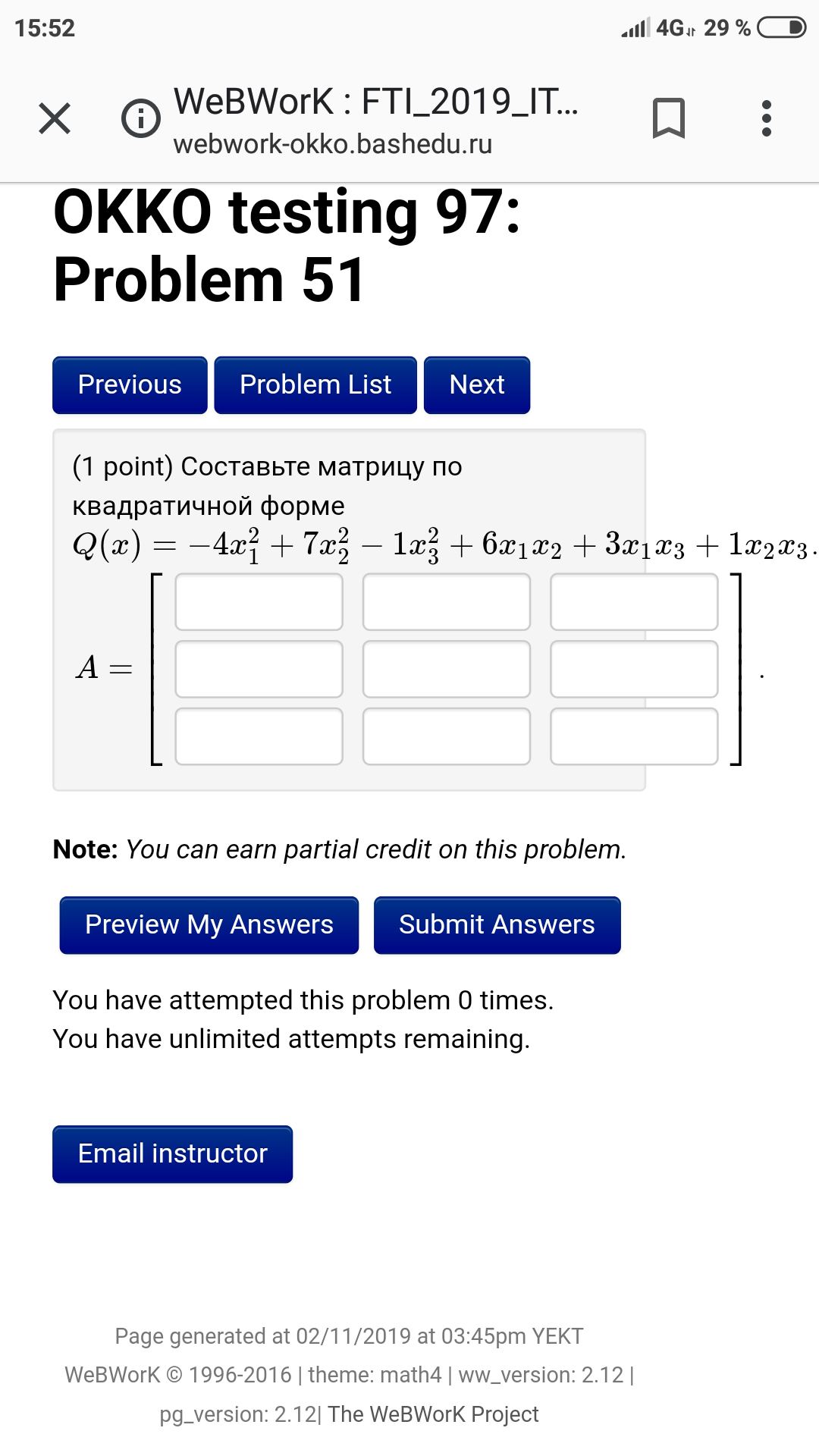
Вычислите, какое из чисел λ = −6 или λ = −5 является собственным числом матрицы A.
Найдите собственный вектор, отвечающий этому собственному числу.
Собственный вектор запишите в виде {p; 2; q}
В ответ введите числа р и q, разделив их точкой с запятой.

1) Пусть А, В и С — множества точек плоскости, заданные характеристическим свойством. Изобразите в системе координат хОу множество D, полученное из множеств А, В и С по формуле δ (Скриншот 1)
2) Существуют ли множества N, Е, Р такие, что выполняется набор условий В? (Скриншот 2)
3) Выяснить взаимное расположение множеств D, Е, F, если А, В, X — произвольные подмножества универсального множества U (Скриншот 3)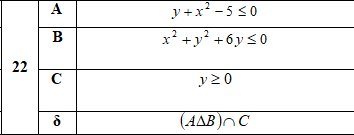

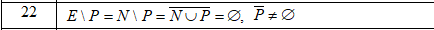
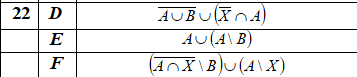
Найди значение матричного многочлена f(A):

1.1.1.12. f(x) = 3x³ + x² + 2, A = ...

Вычислить определитель по правилу «треугольника»:
6 –1 1
2 6 –2
–3 3 6

Условие на картинке

(
2 –1 4 7 1
–6 2 0 –13 –7
–2 0 8 1 –5
8 –3 4 20 8
)

Здравствуйте, очень нужна ваша помощь. Найти собственные значения и собственные векторы матрицы.

Задача 4. Выполнить действия:

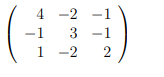
[m]
\left( \begin{matrix}
2 & 4 & 5 \\
3 & 3 & 1 \\
5 & 7 & 1 \\
7 & 5 & 3
\end{matrix} \right)
\cdot
\left( \begin{matrix}
1 & 3 & 5 & 4 \\
4 & -1 & 0 & 2 \\
6 & 0 & 3 & 7
\end{matrix} \right)
-
\left( \begin{matrix}
1 & 3 \\
1 & -4 \\
5 & 0 \\
4 & 1
\end{matrix} \right)
\cdot
\left( \begin{matrix}
2 & 1 & 4 & 5 \\
1 & 0 & 6 & 4 \\
\end{matrix} \right)
[/m]

Задача 1. Вычислить определитель:
| 1 4 2 |
| –7 2 –3 |
| 1 –2 1 |

(8 балл)

Задача 2. Решить систему методом Гаусса
(8 балл)

Задача 3. матричным способом.
{ –x + 3y + 5z = –9
2x – 3y – 7z = 12
2x – 3y – 5z = 10

Составьте матрицу по квадратичной форме [m] Q(x) = -4x_1^2 + 7x_2^2 - 1x_3^2 + 6x_1x_2 + 3x_1x_3 + 1x_2x_3 [/m].

Для данного линейного преобразования найдите обратное

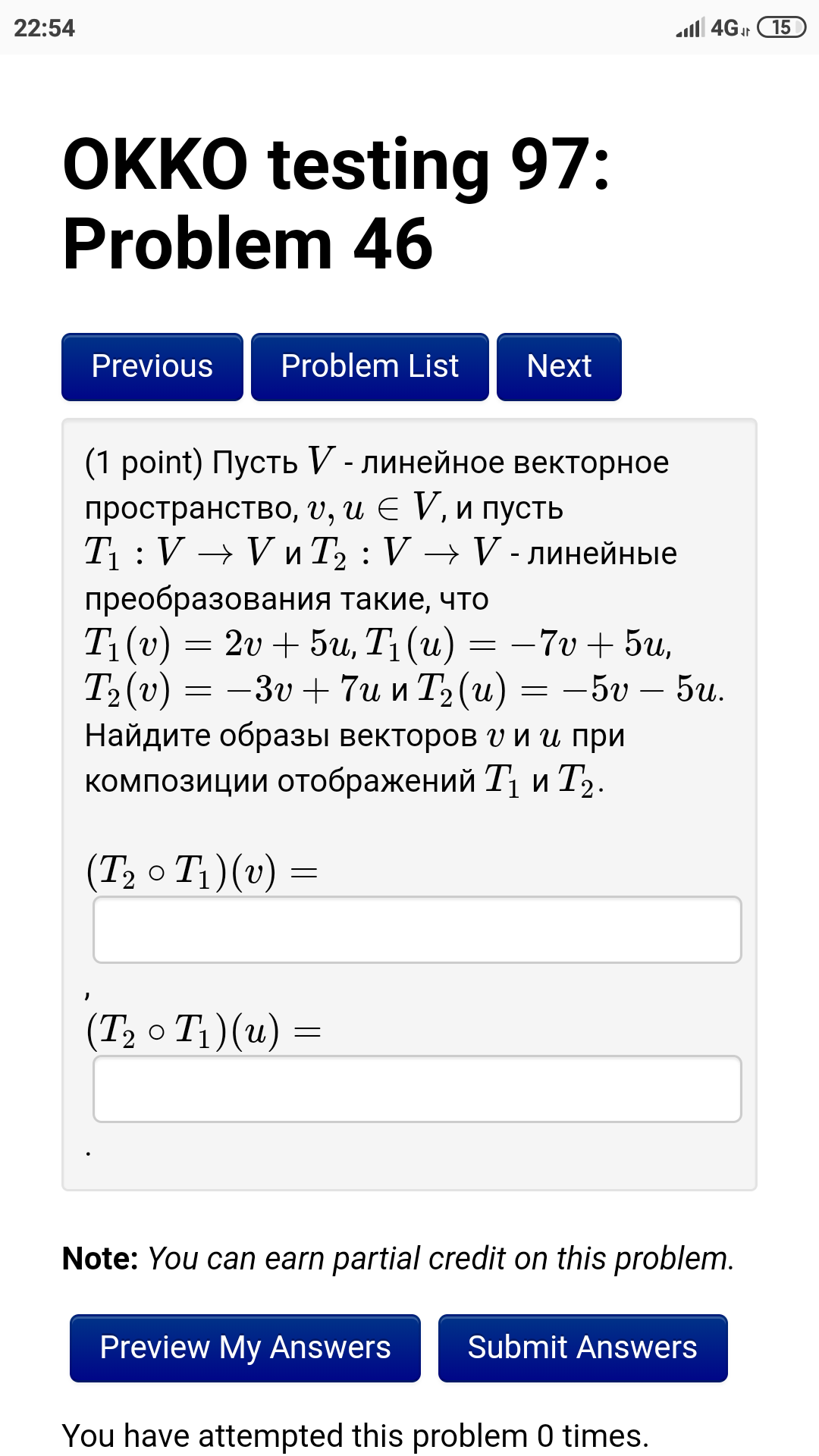
y₁ = 4x₁ – 1x₂
y₂ = –7x₁ + 2x₂

Помогите пожалуйста решить задачу !!!!!!!!!!!!!

Пусть также T : R² → R² – линейное преобразование, которое отображает каждый вектор в вектор av + bw. Найдите матрицу A такую, что T(x) = Ax.

Помогите пожалуйста решить !!!!!!!!

Пусть A = ...

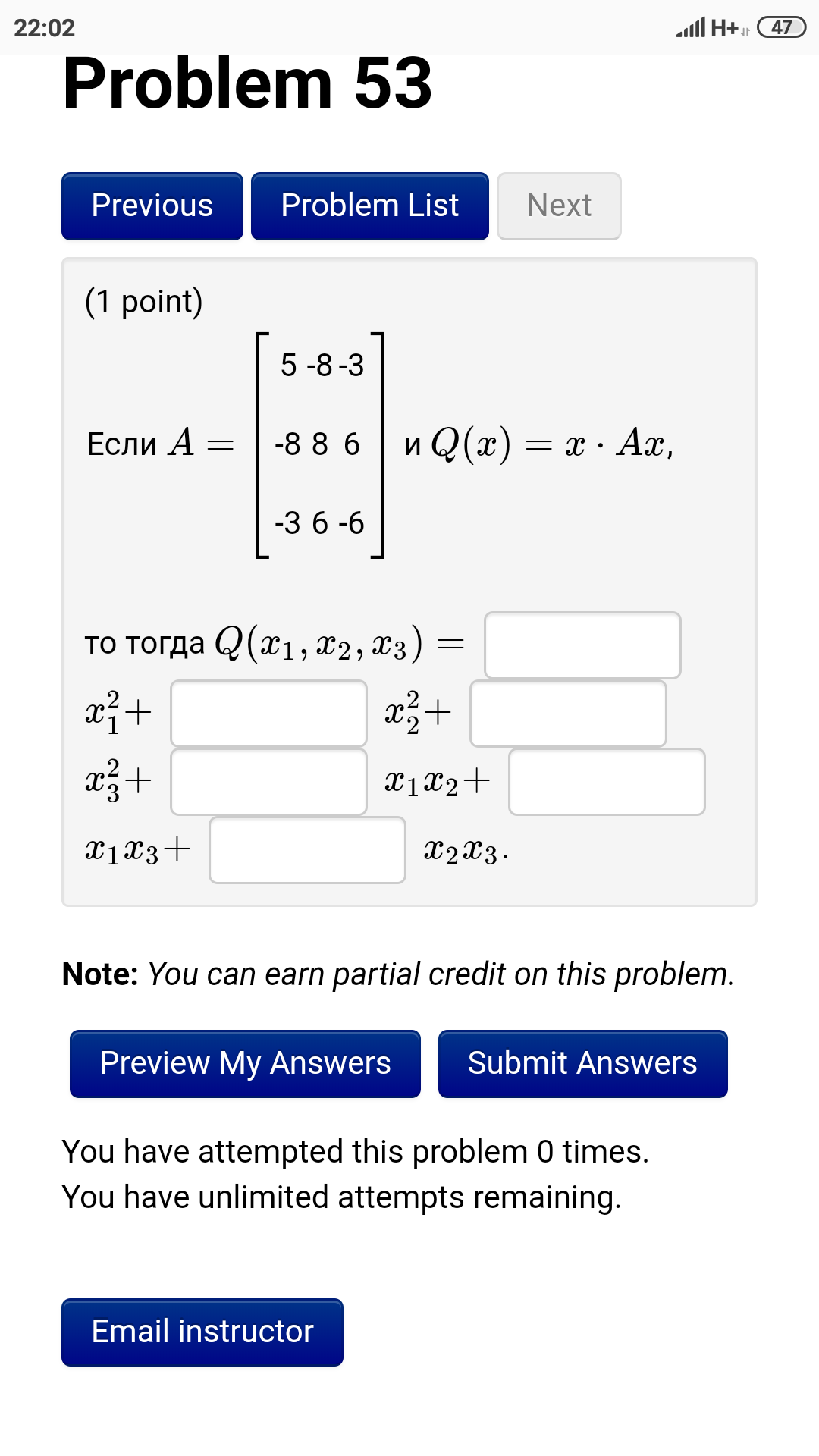
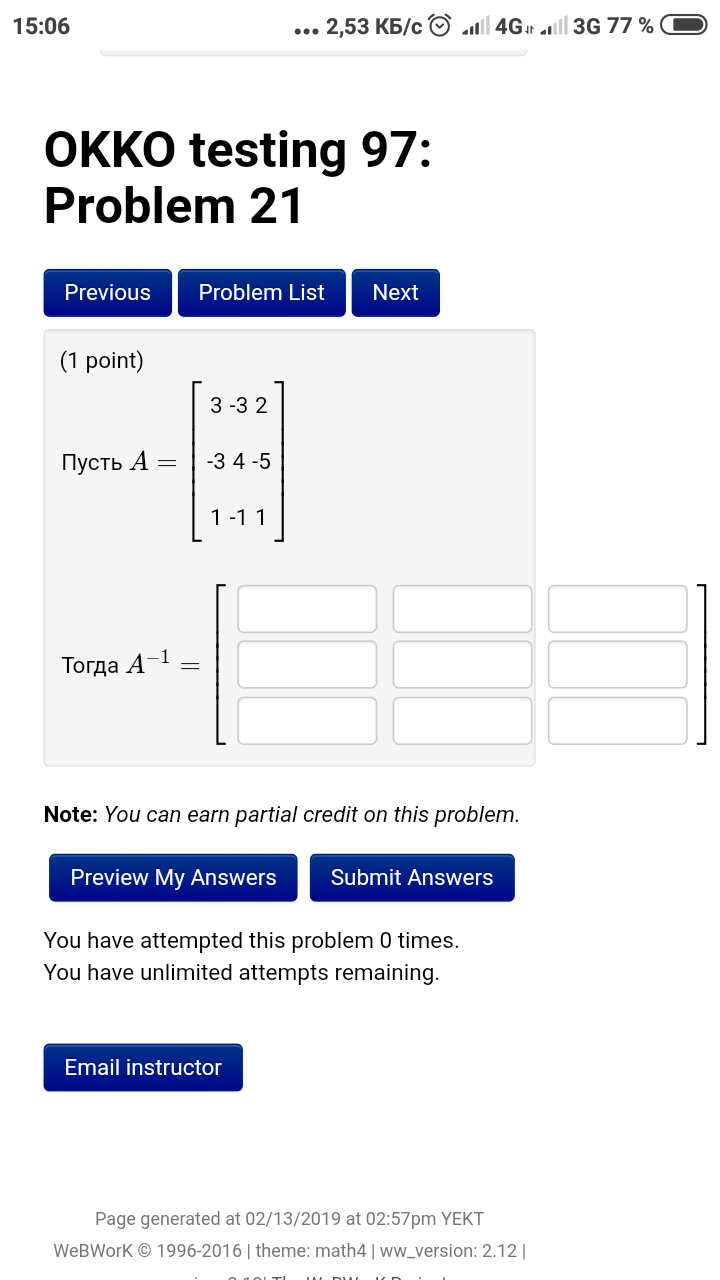
Тогда A^–1 =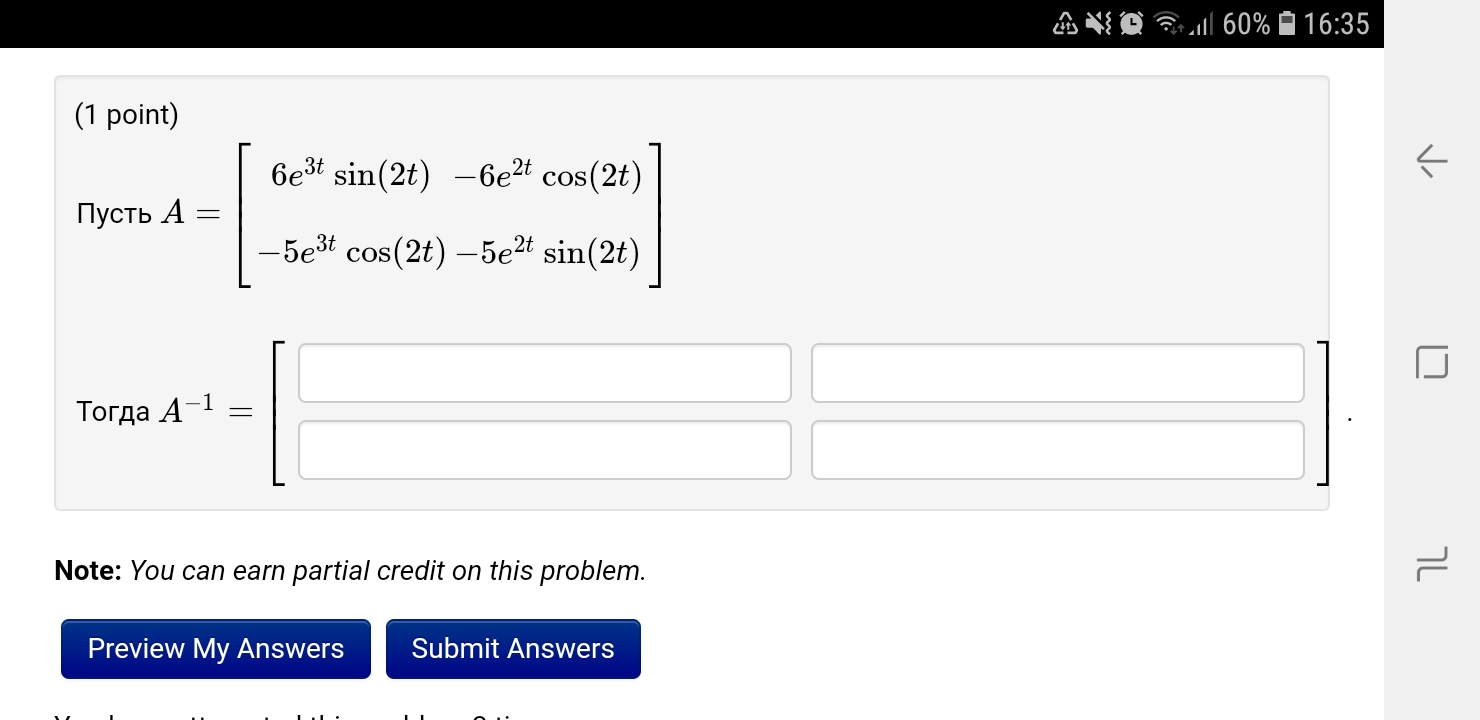

Если A и B матрицы размерности 3×3, det (A) = 5, det (B) = 9, то
det (AB) = 45
det (2A) =
det (A^T) = 5
det (B^–1) = 1/9
det (B²) = 81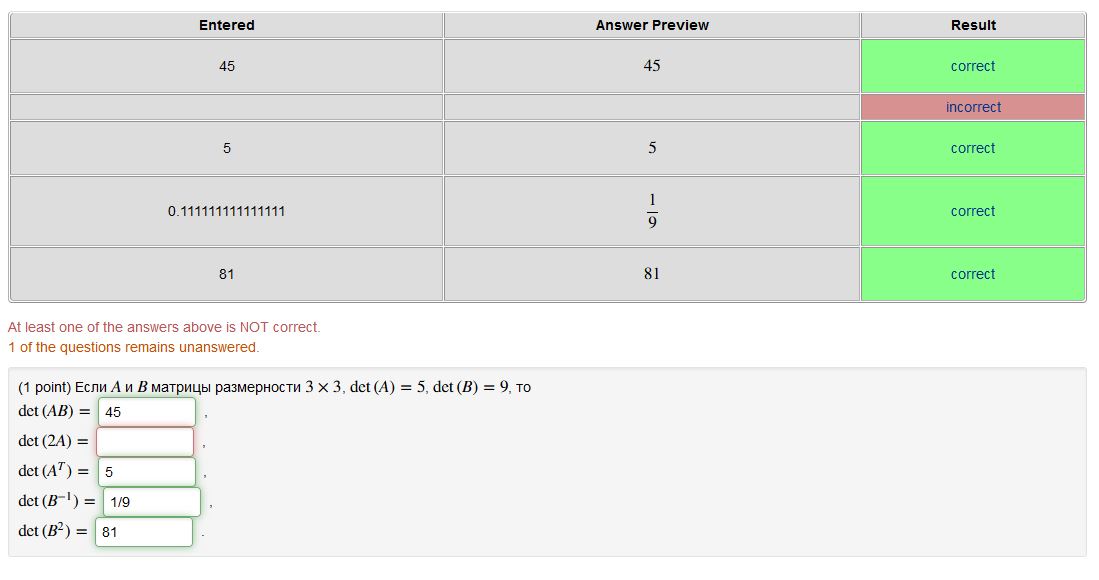

Пусть det ... = 5. Найдите следующие определители :

14. Вычислить определитель третьего порядка по правилу треугольников, разложив по второму столбцу:

| 2 5 3 |
| –1 2 –1 |
| 5 13 5 |.

Пусть L₃ – линейное пространство функций вида y(x) = c₁e^x+c₂xe^x+c₃x²e^x с базисом {e^x, xe^x, x²e^x}. Найдите матрицу оператора А, ставящего в соответствие каждой y(x) принадлежащей L₃ функцию Ay=y(x+1)–y(x–1)

Задание на картинке

Пусть A и B – матрицы размерности 5 × 2, и C – матрица размерности 8 × 5. Какие из следующих алгебраических операций определены?

A. BC
B. CB
C. A^T
D. A^T C^T
E. B – A
F. C – A

Помогите пожалуйста!!!

1 задание

помогите решить матричное уравнение

помогите решить матричное уравнение

помогите найти обратную матрицууу

помогите решить

Помогите с 4

Создатель