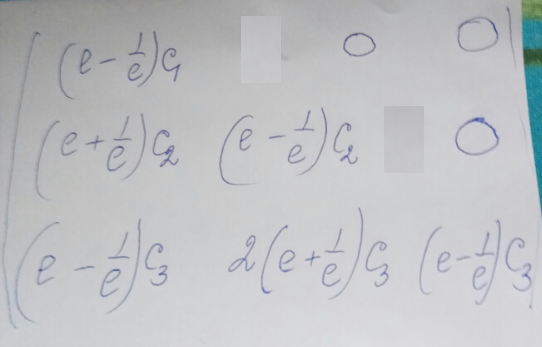Задача 32131 Пусть L_(3 )– линейное пространство...

vk7194275

19 декабря 2018 г. в 14:07

Пусть L₃ – линейное пространство функций вида y(x) = c₁e^x+c₂xe^x+c₃x²e^x с базисом {e^x, xe^x, x²e^x}. Найдите матрицу оператора А, ставящего в соответствие каждой y(x) принадлежащей L₃ функцию Ay=y(x+1)–y(x–1)

sova

19 декабря 2018 г. в 14:25

★

y(x)=(C₁e^x+C₂xe^x+C₃x²e^x
Ay(x)=y(x+1)–y(x–1)=

=C₁·e^x+1+C₂(x+1)·e^x+1+C₃(x+1)²·e^x+1)–

–C₁·e^x–1–C₂(x–1)·e^x–1–C₃(x–1)²·e^x–1)=

=e·C₁e^x+e·C₂xe^x+e·C₂e^x+

+e·C₃x²e^x+2e·C₃xe^x+eC₃e^x–

–(1/e)C₁e^x–(1/e)C₂xe(x)+(1/e)C₂e^x –

–(1/e(C₃x²e^x+(2/e)C₃xe^x – (1/e)C₃e^x=

=(eC₁+eC₂+eC₃–(1/e)C₁+(1/e)C₂–(1/e)C₃)·e^x+

+(eC₂+2eC₃–(1/e)C₂+(2/e)C₃)· x·e^x +

+(eC₃ – (1/e) C₃)·x²e^x