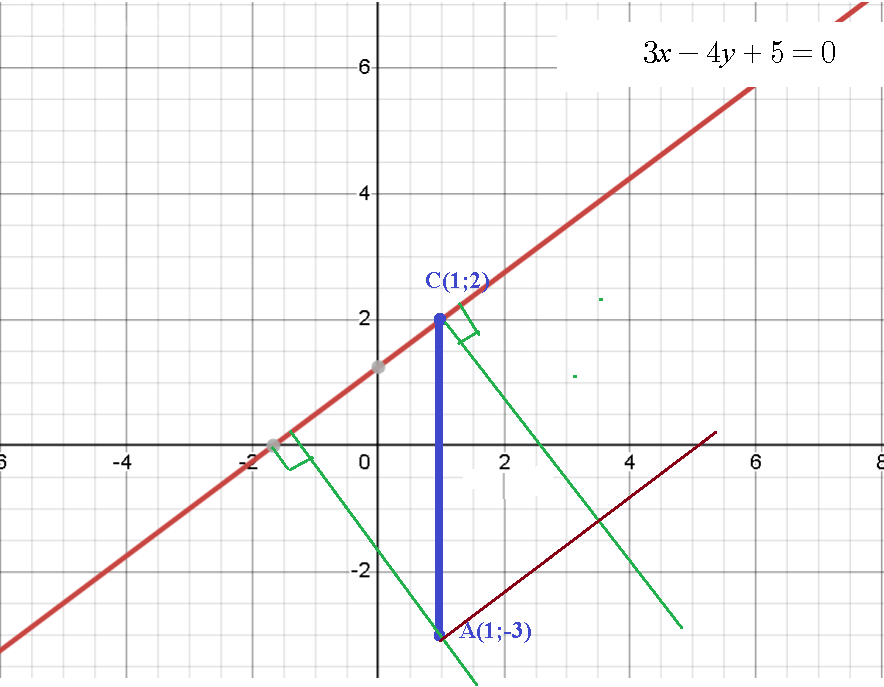
Задача 75225 Даны сторона прямоугольника 3х–4у+5=0 и...

6599400a9ae5ec093245423d

1/6/2024 11:58:04 AM

Даны сторона прямоугольника 3х–4у+5=0 и две его вершины А(1, –3) и С(1, 2). Найти уравнения остальных сторон

5f3ea7e3faf909182968ddd9

1/7/2024 7:35:00 AM

★

3x-4y+5=0 - общее уравнение прямой

Точка С принадлежит этой прямой, так как ее координаты удовлетворяют уравнению:

3*1-4*2+5=0 - верно

Пусть дано уравнение стороны СВ.


Запишем уравнение данной прямой в виде уравнения с угловым коэффициентом

4y=3x+5

y=(3/4)x+(5/4)

k=(3/4)


Прямая AD параллельна CB

Параллельные прямые имеют одинаковые угловые коэффициенты

Значит, уравнение прямой AD имеет вид:

y=(3/4)x+b


Подставим координаты точки А

(1;-3)

-3=(4/3)*1+b

b=-13/3

y=(-4/3)x-(13/3)

4x+3y+13=0 - [b]уравнение стороны AD[/b]


Проводим прямые, перпендикулярные стороне 3x-4y+5=0 и проходящие через точки А и С

Произведение угловых коэффициентов взаимно перпендикулярных прямых равно (-1):

k_(1)*k=-1

k_(1)=-4/3

y=(-4/3)x+b

Подставим координаты точки А

(1;-3)

-3=(-4/3)*1+b

b=-5/3

y=(-4/3)x-(5/3)

4x+3y+5=0 - [b]уравнение стороны AB[/b]

Подставим координаты точки C(1;2)

2=(-4/3)*1+b

b=10/3

y=(-4/3)x+(10/3)

4x+3y-10=0 - [b]уравнение стороны CD[/b]