Задача 75195 Заданы прямые и и точка М. Найти: 1)...

nikola75

2 января 2024 г. в 01:30

Заданы прямые и и точка М.
Найти:
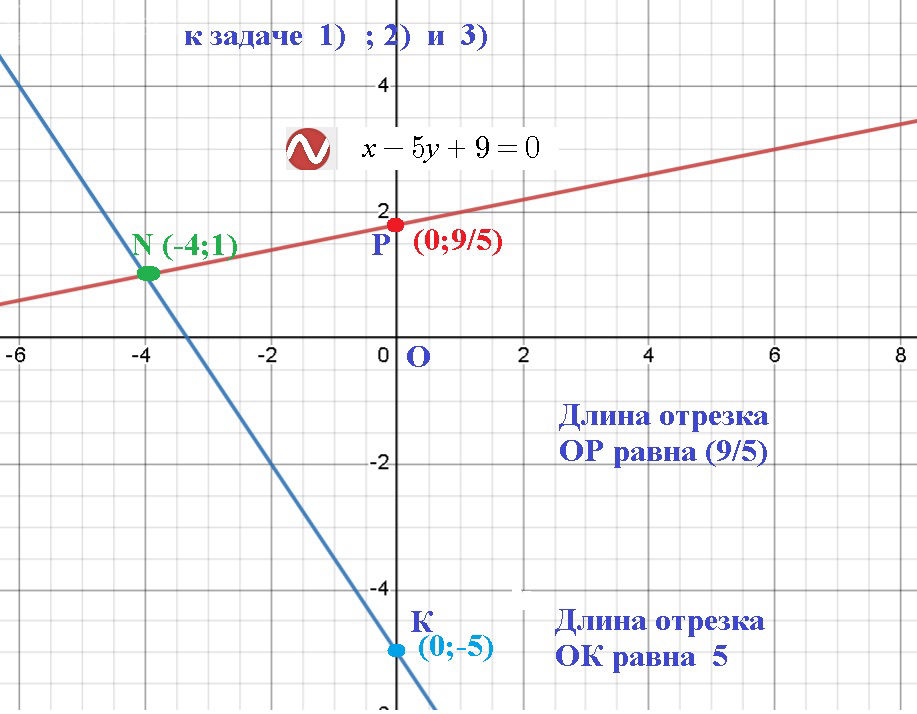
1) угловой коэффициент прямой и отрезок, отсекающий эта прямая на оси ординат;
2) уравнение прямых и в отрезках;
3) точку N пересечения прямых и ;
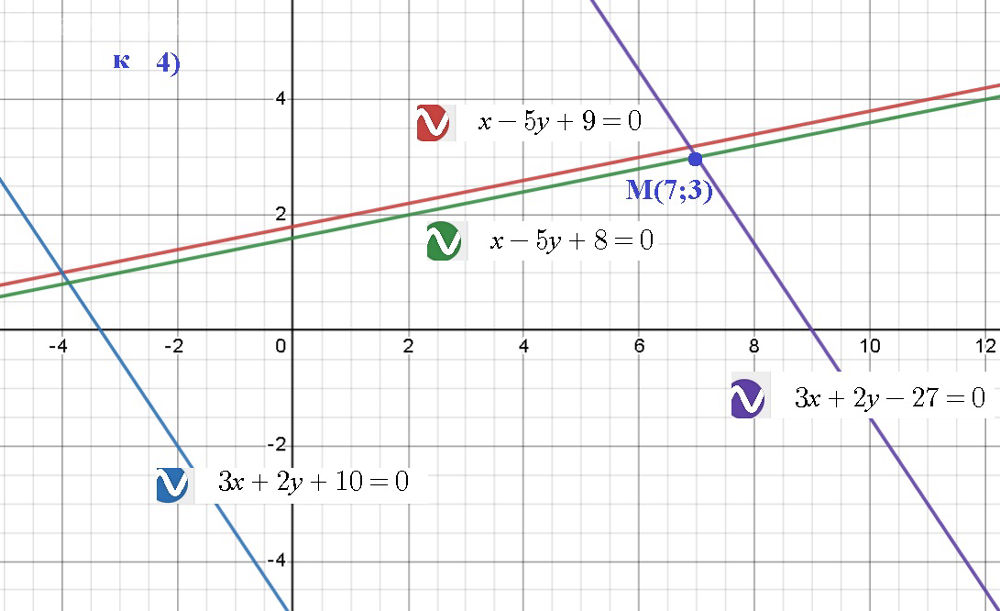
4) уравнение прямой , проходящей через точку М параллельно прямой ;
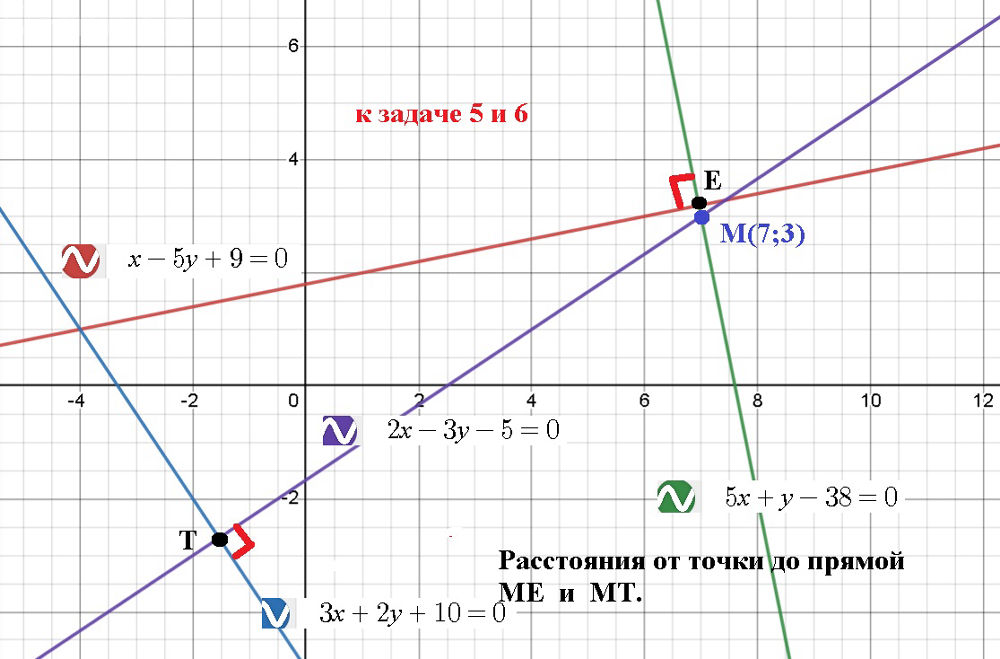
5) уравнение прямой , проходящей через точку М перпендикулярно прямой
6) расстояние от точки М до прямой : r().
Все результаты иллюстрировать графически.
l1: х – 5у + 9 = 0, l2: 3х + 2у + 10 = 0; М(7, 3).

exponenta

2 января 2024 г. в 05:15

★

1) угловой коэффициент прямой и отрезок, отсекающий эта прямая на оси ординат
х – 5у + 9 = 0, ⇒ 5y=x+9 ⇒ y=(1/5)x+(9/5)
угловой коэффициент прямой
k₁=(1/5)
отрезок, отсекающий эта прямая на оси ординат
b₁=(9/5)
3х + 2у + 10 = 0 ⇒ 2y=–3x–10 ⇒ y=(–3/2)x–5
угловой коэффициент прямой
k₂=(–3/2)
отрезок, отсекающий эта прямая на оси ординат
b₂=|–5|=5

2) уравнение прямых в отрезках;

х – 5у + 9 = 0, ⇒ x–5y=–9 Делим на (–9)
(–1/5)x+(5/9)=1

3х + 2у + 10 = 0 ⇒ 3х+2у=–10 Делим на (–10)
(–3/10)x+(–2/10)у=1



3) точку N пересечения прямых

Решаем систему уравнений:
{х – 5у + 9 = 0
{3х + 2у + 10 = 0

Умножаем первое уравнение на (–3)

{–3х +15у –27 = 0
{3х + 2у + 10 = 0

Складываем уравнения


17у–17=0

y=1

Подставляем y=1 в первое уравнение:

х – 5·1 + 9 = 0 ⇒ х=–4

N(–4;1)


4) уравнение прямой , проходящей через точку М(7, 3). параллельно первой прямой

Параллельные прямые имеют одинаковые угловые коэффициенты:
y=(1/5)x+(9/5) ⇒ y=(1/5)x+m₁
Чтобы найти m₁ подставляем координаты точки М:

3=(1/5)·7+m₁ ⇒ m₁=8/5

y=(1/5)x+8/5 ⇒ х–5у+8=0

уравнение прямой , проходящей через точку М(7, 3). параллельно второй прямой
y=(–3/2)x + m₂

подставляем координаты точки М:

3=(–3/2)·7+m₂ ⇒ m₂=27/2

y=(–3/2)x +27/2 ⇒ 3x+2y–27=0


5)
уравнение прямой , проходящей через точку М(7, 3). перпендикулярно первой прямой

Произведение угловых коэффициентов перпендикулярных прямых равно (–1)

k₁·k=–1

(1/5)·k=–1

k=–5

y=–5x+m

подставляем координаты точки М:

3=–5·7+m

m=38

y=–5x+38 –уравнение прямой , проходящей через точку М(7, 3). перпендикулярно первой прямой

Аналогично для второй прямой

k₂·k=–1

k=2/3

y=(2/3)x+m

подставляем координаты точки М:

3=(2/3)·7+m

m=–5/3

y=(2/3)x–(5/3)

2x–3y–5=0 –уравнение прямой , проходящей через точку М(7, 3). перпендикулярно второй прямой

6) расстояние от точки М(7, 3). до прямой :

.х – 5у + 9 = 0,

[m]d_(1)=\frac{|7-5\cdot 3+9|}{\sqrt{1^2+(-5)^2}}[/m]

[m]d_(1)=\frac{1}{\sqrt{26}}[/m]


расстояние от точки М(7, 3). до прямой :

m]d₂=\frac{|3\cdot 7+2\cdot 3+10|}{\sqrt{3²+2²}}[/m]

[m]d_(1)=\frac{37}{\sqrt{13}}[/m]