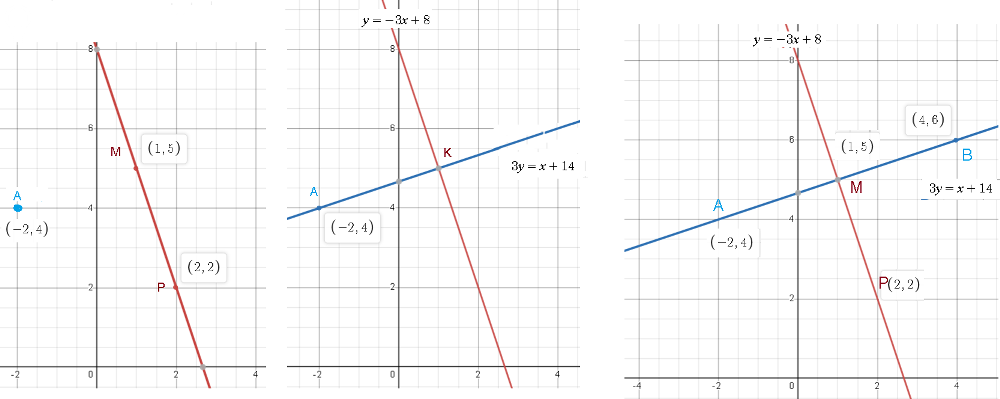
Задача 74428 Найти точку В, симметричную точке...

Нуржигит_642513140

29 ноября 2023 г. в 11:38

Найти точку В, симметричную точке А(–2,4) относительно прямой, проходящей через точки М(1,5) и Р(2,2).

exponenta

30 ноября 2023 г. в 05:40

★

Геометрически:

1)Проводим прямую МР

2)Проводим прямую через точку А перпендикулярно прямой МР.

3)Находим точку К – точку пересечения перпендикуляра и прямой

4) Точка К – середина АВ

АК=КВ



Переводим на язык алгебры

1)
Составляем уравнение прямой МР, проходящей через две точки:

y=kx+b– уравнение прямой с угловым коэффициентом

Подставляем в это уравнение координаты точки М:

M(1;5)

5=k·1+b
Подставляем в это уравнение координаты точки Р:

P(2;2)

2=2k+b

Решаем систему уравнений:

{5=k·1+b
{2=2k+b

3=–k
b=8

y=–3x+ 8 –уравнение прямой МР

2)Провести прямую через точку А перпендикулярно прямой МР,
значит написать уравнение прямой, перпендикулярной прямой АВ и проходящей через точку Р

k_MP=–3

k(AB)·k_MP=–1

k_AB=1/3

y=(1/3)x+b

A(–2;4)

4=(1/3)·(–2)+b

b=4 целых (2/3)

b=14/3

y=(1/3)x+ (14/3) – уравнение прямой, перпендикулярной МР и проходящей через точку А

3)
Найти точку К – точку пересечения прямой МР и перпендикулярной ей прямой, значит
решить систему

{ y=–3x+ 8
{y=(1/3)x+ (14/3)

Приравниваем правые части
–3x+ 8 =(1/3)x+ (14/3)
Умножаем на 3:
–9х+24=х+14

–9х–х=14–24
–10х=–10
х=1

у=–3·1+8

y=5

K(1; 5)=M(1;5)

4)

M– середина отрезка AB

x_M=(1/2)·(x_A+x_B) ⇒ x_A=2x_M–x_A=2·(1)–(–2)=4

y_M=(1/2)·(y_P+y_B) ⇒y_B=2y_M–y_A=2·(5)–4=6

О т в е т. В(4;6)