Задача 74140 Найти предел числовой последовательности...
Условие
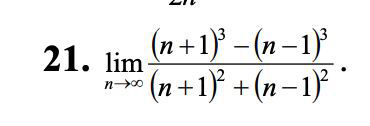
нет в списке колледж
258
Решение
★
[m]=lim_{n → ∞ }\frac{((n+1)-(n-1))((n+1)^2-(n+1)\cdot (n-1)+(n-1)^2}{(n+1)^2+(n-1)^2}=lim_{n → ∞ }\frac{(n+1-n+1)(n^2+2n+1-(n^2-1)+n^2-2n+1}{n^2+2n+1+n^2-2n+1}=[/m]
[m]=lim_{n → ∞ }\frac{2n^2+6}{2n^2+2}=1[/m]