Задача 74139 Найти границу функции по последствиям из...
Условие
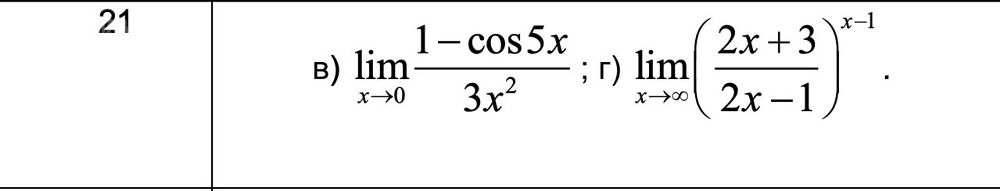
Решение
Применяем первый замечательный предел
По формуле:
[m]1-cos5x=2sin^2\frac{5x}{2}[/m]
[m]lim_{x → 0}\frac{1-cos5x}{3x^2}=lim_{x → 0}\frac{2sin^2\frac{5x}{2}}{3x^2}=\frac{2}{3}lim_{x → 0}\frac{sin\frac{5x}{2}}{\frac{5x}{2}}\cdot \frac{sin\frac{5x}{2}}{\frac{5x}{2}}\cdot\frac{ \frac{5x}{2}\cdot \frac{5x}{2}}{x^2}=\frac{2}{3}\cdot 1\cdot 1\cdot \frac{5}{2}\cdot \frac{5}{2}=\frac{25}{6}[/m]
г)неопределенность (1^( ∞ ))
Применяем второй замечательный предел
[m]\lim_{x \to\infty}(\frac{2x+3}{2x-1})^{x-1}=\lim_{x \to\infty}(1+\frac{4}{2x-1})^{\frac{2x-1}{4}})^{\frac{4(x-1)}{2x-1}} =[/m]
[m]\lim_{x \to\infty}(1+\frac{4}{2x-1})^{\frac{2x-1}{4}})^{\lim_{x \to\infty}\frac{4(x-1)}{2x-1}}=e^2[/m]