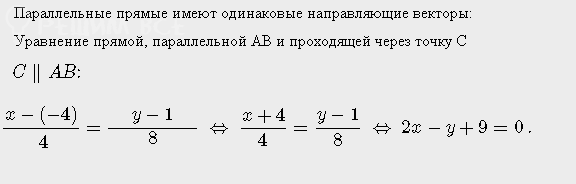Задача 73500 Даны вершины треугольника...
Условие
Найти :
а)уравнение стороны AB
б)уравнение высоты CH
в)уравнение медианы АМ
г) точку N пересечения медианы АМ и высоты СН
д)уравнение прямой проходящей через вершину С параллельно стороне АВ
е)расстояние от точки С до прямой АВ
А(6,-9);В(10,-1);С(-4,1)
Решение
имеет вид:
[m]\frac{x-x_{A}}{x_{B}-x_{A}}=\frac{y-y_{A}}{y_{B}-y_{A}}[/m]
Подставим координаты точек А и В:
[m]\frac{x-6}{10-6}=\frac{y-(-9)}{-1-(-9)}[/m] ⇒ [m]\frac{x-6}{4}=\frac{y+9}{8}[/m]
[m]8(x-6)=4(y+9)[/m]
[m]2(x-6)=y+9[/m]
[m]2x-y-21=0[/m] - общее уравнение прямой AB
2) уравнение высоты, проведенной из вершины С
Высота, проведенная из вершины С перпендикулярна стороне АВ
Запишем уравнение стороны АВ как уравнение прямой с угловым коэффициентом k
[m]2x-y-21=0[/m]⇒ [m]y=2x-21[/m]⇒ [m]k=2[/m] - угловой коэффициент прямой АВ
k_(AB)=2
Произведение угловых коэффициентов взаимно перпендикулярных прямых равно (-1)
k_(AB)*k_(CH)=-1
k_(CH)=[m]-\frac{1}{2}[/m]
[m]y=-\frac{1}{2}x+b[/m] - уравнение любой прямой, перпендикулярной АВ
Подставляем координаты точки C
[m]1=-\frac{1}{2}\cdot (-4)+b[/m]
[m]b=3[/m]
[m]y=-\frac{1}{2}x+3[/m]- уравнение высоты CH
3) уравнение медианы АМ
Находим координаты точки М - середины BС
x_(М)=[m]\frac{(x_{B}+x_{C}}{2}=3[/m]
y_(М)=[m]\frac{(y_{B}+y_{C}}{2}=0[/m]
уравнение медианы АМ как прямой, проходящей через две точки
имеет вид:
[m]\frac{x-x_{A}}{x_{M}-x_{A}}=\frac{y-y_{A}}{y_{M}-y_{A}}[/m]
Подставим координаты точек А и M:
[m]\frac{x-6}{3-6}=\frac{y-(-9)}{0-(-9)}[/m] ⇒ [m]\frac{x-6}{(-3)}=\frac{y+9}{9}[/m]
[m]9(x-6)=-3(y+9)[/m]
[m]3(x-6)=-y-9[/m]
[m]3x+y-9=0[/m]
- уравнение медианы АМ
4)
Чтобы найти координаты точки N решаем систему
{[m]y=-\frac{1}{2}x+3[/m]
{ [m]3x+y-9=0[/m]
[m]3x-\frac{1}{2}x+3-9=0[/m] ⇒ [m]\frac{5}{2}x=6[/m] ⇒ [m]x=\frac{12}{5}[/m]
[m]x=2,4[/m]
[m]y=-\frac{1}{2}\cdot 2,4+3[/m]
[m]y=1,8[/m]