Задача 72046 Составить уравнение прямой, отстоящей от...

Linkkkk

14 июня 2023 г. в 08:47

Составить уравнение прямой, отстоящей от точки (1, 1) на расстоянии 2, а от точки (2, 3)
на расстоянии 4.

exponenta

14 июня 2023 г. в 11:28

★

Для простоты решения сдвинуть окружности так, чтобы центр одной окружности был в точке (0;0)

(1;1) → (0;0)

Тогда центр второй окружности

(2;3) → (1;2)

Получим уравнения:

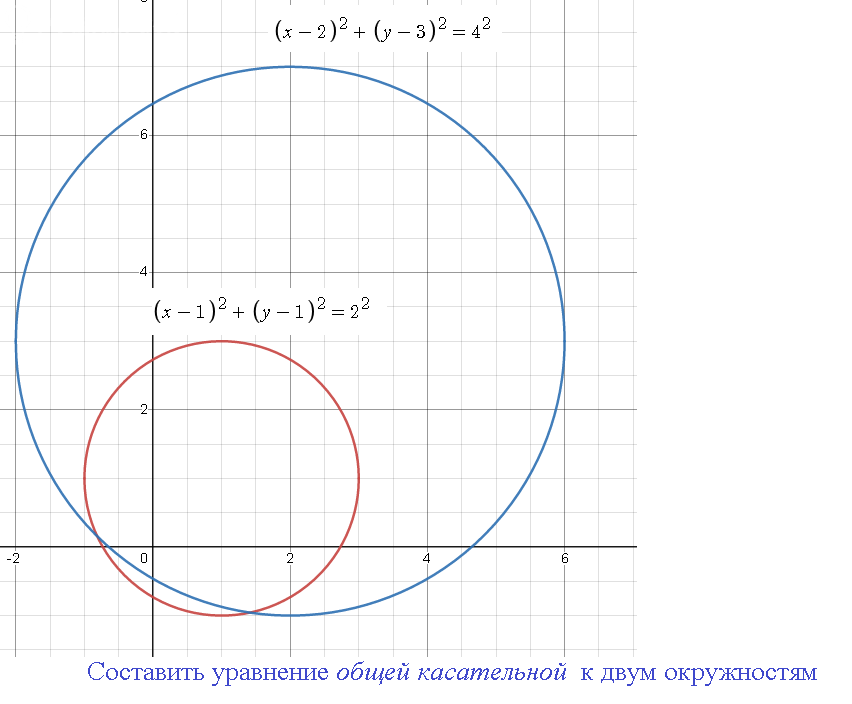
x²+y²=4


(x–1)²+(y–2)²=16

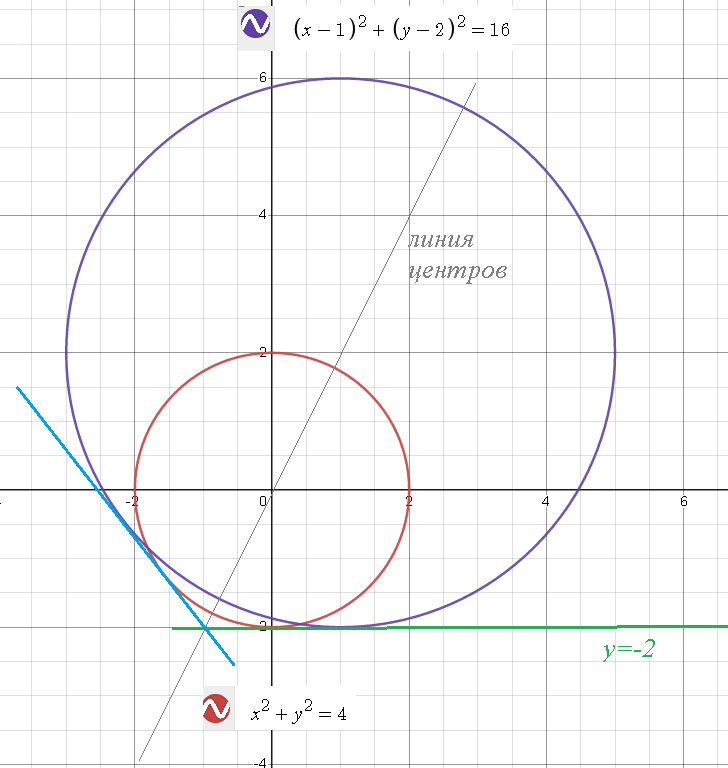
y=–2 – одна касательная

В самом деле: расстояние от центра первой окружности до прямой равно 2, от центра второй окружности равно 4

Вторая касательная образует с линией центров такой же угол, как и прямая y=–2

Составляем уравнение линии центров

y=2x


Находим угол между линией центров и касательной.

tg α =k=2

для второй касательной этот коэффициент с минусом

y=–2x+b








Уравнение для исходного случая, y=–1