Задача 71895 Продифференцировать данные функции...
Условие
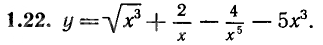
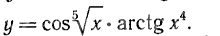
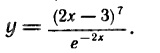
Решение
[m]y`=(\sqrt{x^3}+\frac{2}{x}-\frac{4}{x^5}-5x^3)`=[/m]
производная суммы ( разности) равна сумме (разности) производных
[m]=(\sqrt{x^3})`+(\frac{2}{x})-(\frac{4}{x^5})`-(5x^3)`=[/m]
постоянный множитель можно выносить за знак производной:
[m]=(\sqrt{x^3})`+2(\frac{1}{x})-4(\frac{1}{x^5})`-5(x^3)`=[/m]
применяем свойства степени:
[m]=(x^{\frac{3}{2}})`+2(x^{-1})`-4(x^{-5})`-5(x^3)`=[/m]
применяем формулу производная степени:
[r][m](x^{ α })`= α \cdot x^{ α -1}[/m][/r]
[m]=\frac{3}{2}\cdot x^{\frac{3}{2}-1} +2\cdot (-1)x^{-1-1}-4\cdot (-5)\cdot x^{-5-1}-5\cdot 3\cdot x^{3-1}=[/m]
[m]=\frac{3}{2}\cdot x^{\frac{1}{2}}-2x^{-2}+20x^{-6}-15x^2=[/m]
[m]=\frac{3}{2}\sqrt{x}-\frac{2}{x^2}+\frac{20}{x^{6}}-15x^2[/m] - это ответ
б)
[m]y=cos\sqrt[5]{x}\cdot arctg x^4[/m]
Применяем правило дифференцирования произведения:
[r][m](uv)`=u`v+uv`[/m][/r]
[m]y`=(cos\sqrt[5]{x})`\cdot arctg x^4+cos\sqrt[5]{x}\cdot (arctg x^4)`[/m]
применяем таблицу производных сложной функции
[r][m](cosu )`=-sinxu\cdot u`[/m][/r]
[r][m](arctgu )`=\frac{1}{1+u^2}\cdot u`[/m][/r]
[m]y`=-sin\sqrt[5]{x}\cdot (\sqrt[5]{x})`\cdot arctg x^4+cos\sqrt[5]{x}\cdot\frac{1}{1+(x^4)^2}\cdot (x^4)`[/m]
[m]y`=-sin\sqrt[5]{x}\cdot \frac{1}{5}x^{\frac{1}{5}-1}\cdot arctg x^4+cos\sqrt[5]{x}\cdot\frac{1}{1+x^8}\cdot (4x^3)[/m]
[m]y`=-\frac{1}{5} \cdot sin\sqrt[5]{x}\cdot x^{-\frac{4}{5}}\cdot arctg x^4+cos\sqrt[5]{x}\cdot\frac{4x^3}{1+x^8}[/m]- о т в е т
в)
[m]y=\frac{(2x-3)^7}{e^(-2x)}[/m]
Применяем правило дифференцирования дроби (частного)
:
[r][m](\frac{u}{v})`=\frac{u`v-uv`}{v^2}[/m][/r]
[m]y=\frac{((2x-3)^7)`\cdot e^{-2x}-(x^4+1)\cdot (e^{-2x})`}{(e^{-2x})^2}[/m]
применяем таблицу производных сложной функции
[r][m](u^{ α })`= α \cdot u^{ α -1}\cdot u`[/m][/r]
[r][m](e^{ u })`= e^{u} \cdot u`[/m][/r]
[m]y`=\frac{7\cdot (2x-3)^6\cdot e^{-2x}-(2x-3)^7\cdot e^{-2x}\cdot (-2x)`)}{e^{-4x}}[/m]
[m]y`=\frac{(2x-3)^6\cdot e^{-2x}\cdot (7 -(2x-3)\cdot (-2))}{e^{-4x}}[/m]
[m]y`=\frac{(2x-3)^6\cdot (1+4x)}{e^{-2x}}[/m] - о т в е т