Задача 71888 Решить пределы. Весь номер полностью...
Условие
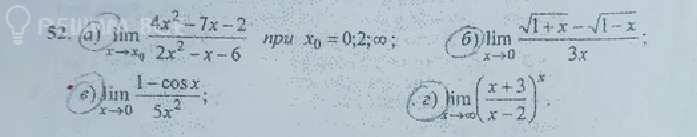
Решение
a)
[m]\lim_{x \to x_{o} }\frac{4x^2-7x-2}{2x^2-x-6}=[/m]
[m]x_{o}=0[/m]
[m]\lim_{x \to x_{o} }\frac{4x^2-7x-2}{2x^2-x-6}=\frac{4\cdot 0^2-7\cdot 0-2}{2\cdot 0^2-0-6}=\frac{(-2)}{(-6)}=\frac{1}{3}[/m]
[m]x_{o}=2[/m]
[m]\lim_{x \to 2 }\frac{4x^2-7x-2}{2x^2-x-6}=\frac{4\cdot 2^2-7\cdot 2-2}{2\cdot 2^2-2-6}=\frac{0}{0}[/m]
неопределенность.
Раскладываем на множители и числитель и знаменатель:
[m]=\lim_{x \to 2 }\frac{(x-2)(4x+1)}{(x-2)(2x+3)}=[/m]
сокращаем на [m](x-2)[/m]
[m]=\lim_{x \to 2 }\frac{4x+1}{2x+3}=\frac{4\cdot 2+1}{2\cdot 2+3}=\frac{9}{7}[/m]
[m]x_{o}=\infty [/m]
[m]\lim_{ \to \infty }\frac{4x^2-7x-2}{2x^2-x-6}=\frac{∞}{∞}[/m]
Неопределенность.
Делим числитель и знаменатель на x^2:
[m]=\lim_{ \to \infty }\frac{\frac{4x^2-7x-2}{x^2}}{\frac{2x^2-x-6}{x^2}}=[/m]
Делим [i] почленно[/i], те каждое слагаемое числителя делим на [m]x^2[/m] и
каждое слагаемое знаменателя делим на [m]x^2[/m]:
[m]=\lim_{ \to \infty }\frac{\frac{4x^2}{x^2}-\frac{7x}{x^2}-\frac{2}{x^2}}{\frac{2x^2}{x^2}-\frac{x}{x^2}-\frac{6}{x^2}}=[/m]
[m]=\lim_{ \to \infty }\frac{4-\frac{7}{x}-\frac{2}{x^2}}{2-\frac{1}{x}-\frac{6}{x^2}}=\frac{4-0-0}{2-0-0}=\frac{4}{2}=2[/m]
б)
[m]lim_{x→ 0 }\frac{\sqrt{1+x}-\sqrt{1-x}}{3x}=\frac{\sqrt{1+0}-\sqrt{1-0}}{3\cdot 0}=\frac{0}{0} [/m]-неопределенность/
Умножаем на [m] (\sqrt{1+x}+\sqrt{1-x}) [/m] и числитель и знаменатель:
[m]lim_{x→ 0}\frac{(\sqrt{1+x}-\sqrt{1-x})\cdot (\sqrt{1+x}+\sqrt{1-x})}3x{\sqrt{1-x}+\sqrt{1+x}}=lim_{x→0 }\frac{(\sqrt{1+x})^2-(\sqrt{1-x})^2}{\sqrt{1+x}+\sqrt{1-x}}=[/m]
[m]=lim_{x→0}\frac{1+x-1+x}{3x\cdot \sqrt{1+x}+\sqrt{1-x}}=[/m]
[m]=lim_{x→0 }\frac{2}{3\sqrt{1+x}+\sqrt{1-x}}=\frac{2}{3\sqrt{1+0}+\sqrt{1-0}}=\frac{2}{3}[/m]
в)
[m]lim_{x → 0}\frac{1-cosx}{5x^2}=\frac{1-cos0}{0}=\frac{1-1}{0}=\frac{0}{0}-[/m] неопределенность
Применяем первый замечательный предел
[m]=lim_{x → 0}\frac{2sin^2\frac{x}{2}}{5x^2}=\frac{2}{5}lim_{x → 0}\frac{sin\frac{x}{2}\cdot sin\frac{x}{2}}{2\cdot \frac{x}{2}\cdot \frac{x}{2}\cdot 2}=\frac{2}{5}\cdot \frac{1}{2\cdot 2}\cdot lim_{x → 0}\frac{sin\frac{x}{2}}{ \frac{x}{2} }lim_{x → 0}\frac{sin\frac{x}{2}}{ \frac{x}{2} }=\frac{1}{10}\cdot 1\cdot 1=\frac{1}{10}[/m]
г)
[m]lim_{x → ∞ }(\frac{x+3}{x-2})^{x}=[/m]
[m]lim_{x → ∞ }\frac{x+3}{x-2}=\frac{ ∞ }{ ∞ }[/m]
неопределенность, делим числитель и знаменатель на [m]x[/m]
[m]=lim_{x → ∞ }\frac{\frac{x+3}{x}}{\frac{x-2}{x}}=[/m]
делим[i] почленно[/i] , т.е. каждое слагаемое числителя делим на [m]x[/m] и
каждое слагаемое знаменателя делим на [m]x[/m]:
[m]=lim_{x → ∞ }\frac{\frac{x}{x}+\frac{3}{x}}{\frac{x}{x}-\frac{2}{x}}=lim_{x → ∞ }\frac{1+\frac{3}{x}}{1-\frac{2}{x}}=\frac{1+0}{1-0}=1[/m]
[m]lim_{x → ∞ }(\frac{x+3}{x-2})^{x}=1^{ ∞} [/m] неопределенность
Применяем второй замечательный предел
[m]=lim_{x → ∞ }(\frac{1+\frac{3}{x}}{1-\frac{2}{x}})^{x}=\frac{lim_{x → ∞ }(1+\frac{3}{x})^{x}}{lim_{x → ∞ }(1-\frac{2}{x})}=\frac{e^{3}}{e^{-2}}=e^{3-(-2)}=e^{5}[/m]
Не размещайте 6 задач в одном вопросе. Это занимает много места и тратится лишнее время на просмотр своего же решения.