Задача 71834 Производная сложной функции y =...
Условие
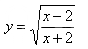
Решение
[m]y=\sqrt{u}[/m] ⇒ [m]y`=\frac{1}{2\sqrt{u}}\cdot (u`)[/m]
[m]y=\sqrt{\frac{x-2}{x+2}}[/m] ⇒ [m]y`=\frac{1}{2\sqrt{\frac{x-2}{x+2}}}\cdot (\frac{x-2}{x+2})`=[/m]
Применяем формулу дифференцирования частного:
[m](\frac{u}{v})`=\frac{u`\cdot v-u\cdot v`}{v^2}[/m]
⇒
[m]y`=\frac{1}{2\sqrt{\frac{x-2}{x+2}}}\cdot \frac{(x-2)`\cdot (x+2)-(x-2)\cdot (x+2)`}{(x+2)^2}[/m]
[m]y`=\frac{\sqrt{x+2}}{2\sqrt{x-2}}\cdot \frac{ (x+2)-(x-2)}{(x+2)^2}[/m]
[m]y`=\frac{\sqrt{x+2}}{2\sqrt{x-2}}\cdot \frac{ x+2-x+2}{(x+2)^2}[/m]
[m]y`=\frac{\sqrt{x+2}}{2\sqrt{x-2}}\cdot \frac{ 4}{(x+2)^2}[/m]
[m]y`=\frac{\sqrt{x+2}}{\sqrt{x-2}}\cdot \frac{ 2}{(x+2)^2}[/m]
[m]y`= \frac{ 2}{\sqrt{(x-2)(x+2)^3}}[/m]