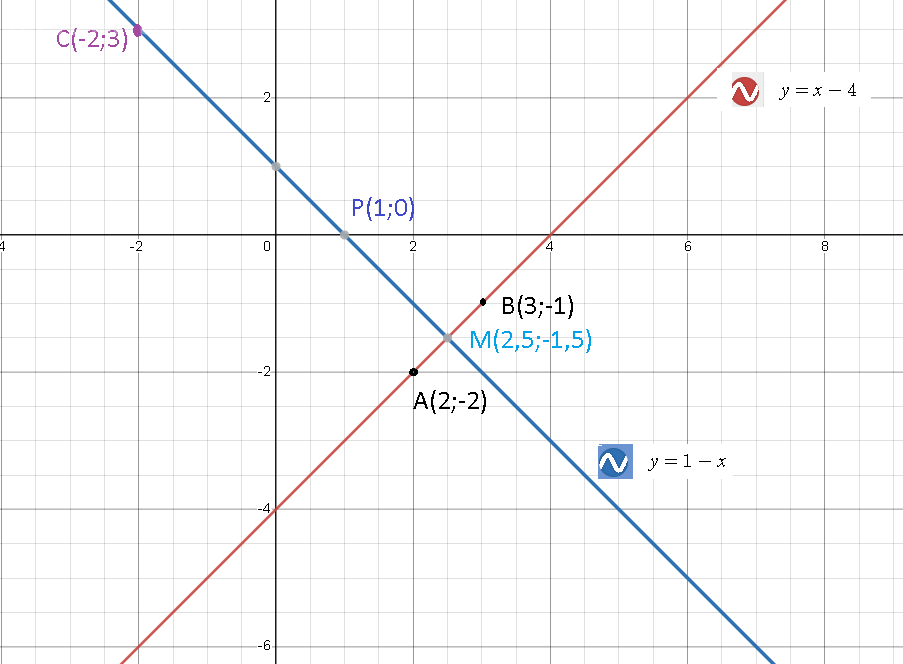
Задача 68142 Даны две вершины А(2;–2) и В(3;–1) и...

63bacdd112a36b2f63c6198e

08.01.2023 17:43:53

Даны две вершины А(2;–2) и В(3;–1) и точка Р(1;0) пересечения медиан
треугольника ABC. Составить уравнение высоты треугольника, проведенной
через третью вершину С. Сделать чертеж.

5f3ea7e3faf909182968ddd9

08.01.2023 23:26:15

★

Найдем координаты точки М- середины АВ

x_(M)=(x_(A)+x_(В))/2=(2+3)/2=2,5

y_(M)=(y_(A)+y_(В))/2=(-2+(-1))/2=-1,5


Составляем уравнение прямой РМ - медианы из точки С

[m]\frac{x-1}{2,5-1}=\frac{y-0}{-1,5-0}[/m] ⇒ y=1-x


Находим координату точки С по формуле деления отрезка в данном отношении

CP:PM=2:1

x_(P)=(x_(C)+[red]2[/red]*x_(M))/1+[red]2[/red]) ⇒ x_(C)=3x_(P)-2x_(M)=3-5=[b]-2[/b]

y_(P)=(y_(C)+[red]2[/red]*y_(M))/(1+[red]2[/red])= ⇒ y_(C)=3y_(P)-2y_(M)=[b]3[/b]



Составляем уравнение высоты как прямой, перпендикулярной АВ и проходящей через точку С


Составим уравнение прямой АВ:

[m]\frac{x-2}{3-2}=\frac{y+2}{-1+2}[/m] ⇒ y=x-4

Произведение угловых коэффициентов взаимно перпендикулярных прямых равно (-1)

Перпендикулярная прямая имеет угловой коэффициент k=-1

y=-x+b

Чтобы найти b подставим координаты точки С

3=-(-2)+b

b=1


y=-x+1 - уравнение высоты

Это уравнение совпадает с уравнением медианы из точки С