Задача 68097 Задача 3 1. Даны уравнения двух сторон...

63b5a5c761079b77ceefa6fe

04.01.2023 19:41:36

Задача 3
1. Даны уравнения двух сторон параллелограмма 8x+3y +
+ 1 = 0, 2x + y − 1 = 0 и уравнение одной из его диагоналей
3x + 2y + 3 = 0. Определить координаты вершин этого параллелограмма.
3. Найти координаты точки, симметричной точке A(5; 2) относительно прямой 4x + 2y + 1 = 0.

5f3ea7e3faf909182968ddd9

04.01.2023 20:00:39

★

Находим координаты вершины параллелограмма как точки пересечения двух сторон

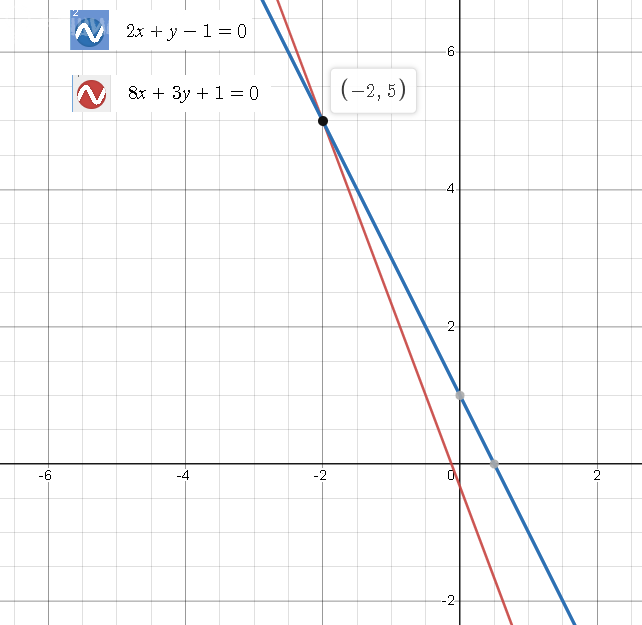
Решаем систему двух уравнений:
{8x+3y + 1 = 0,
{2x + y − 1 = 0
Умножаем второе уравнение на (-3)

{8x+3y + 1 = 0,
{-6x -3 y +3 = 0

складываем

2х+4=0

х=-2
y=-2x+1
y=5

Пусть это точка А (-2;5)

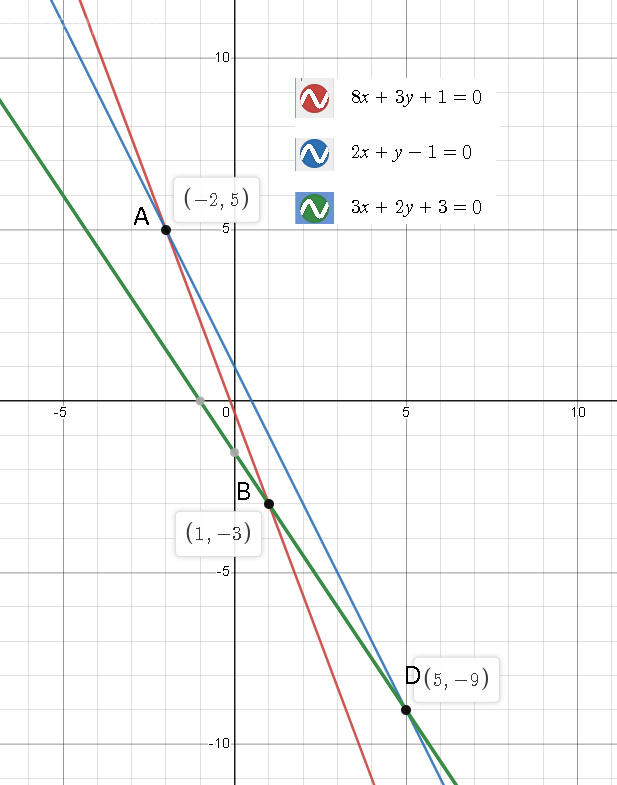
Аналогично, находим координаты вершин B и D параллелограмма как точки пересечения диагонали и стороны
Решаем две системы двух уравнений:
{8x+3y + 1 = 0,
{3x+2y+3=0

...решайте самостоятельно

Получим точку В (1;-3)


{2x + y − 1 = 0
{3x+2y+3=0

... решайте самостоятельно

Получим точку D(5;-9)

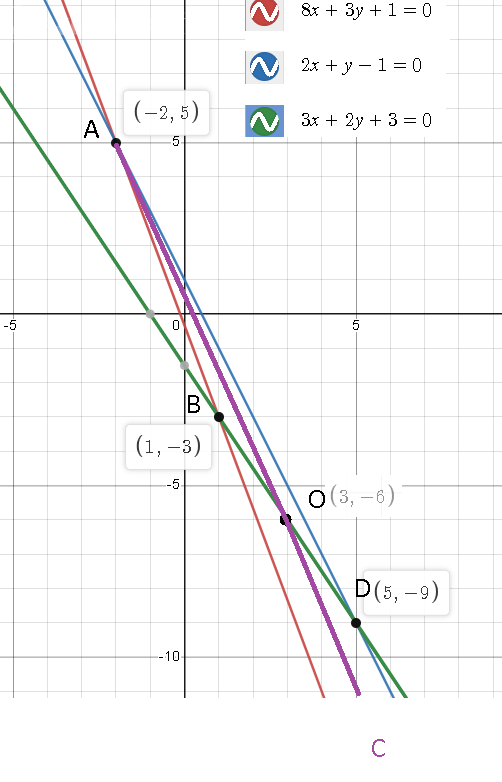
Найдем середину диагонали BD

x_(O)=(x_(B)+x_(D))/2=(1+5)/2=3

y_(O)=(y_(B)+y_(D))/2=(-3+(-9))/2=-6

[b]O ( 3; -6)[/b]


Найдем координаты точки С
x_(O)=(x_(A)+x_(C))/2
y_(O)=(y_(A)+y_(C))/2

⇒
x_(C)=2x_(O)-x_(A)=2*3-(-2)=8
y_(C)=2y_(O)-y_(A)=2*(-6)-5=-17

[b]С(8;-17)[/b]